题目内容
(本题满分12分)
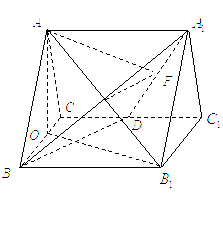 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点。(Ⅰ)求证:AB1⊥面A1BD;
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点。(Ⅰ)求证:AB1⊥面A1BD;
(Ⅱ)求二面角A-A1D-B的大小;
(Ⅲ)求点C到平面A1BD的距离;
(Ⅰ)略(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
解析:
:解法一:(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() 为正三角形,
为正三角形,![]() .
.
![]() 正三棱柱
正三棱柱![]() 中,
中,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
连结![]() ,在正方形
,在正方形![]() 中,
中,![]() 分别为
分别为
![]() 的中点,
的中点,![]() ,
,![]() .
.
在正方形![]() 中,
中,![]() ,
,![]() 平面
平面![]() .
.
(Ⅱ)设![]() 与
与![]() 交于点
交于点![]() ,在平面
,在平面![]() 中,作
中,作![]() 于
于![]() ,连结
,连结![]() ,由(Ⅰ)得
,由(Ⅰ)得![]() 平面
平面![]() .
.![]() ,
,![]() 为二面角
为二面角![]() 的平面角.在
的平面角.在![]() 中,由等面积法可求得
中,由等面积法可求得![]() ,又
,又![]() ,
,
 .
.
所以二面角![]() 的大小为
的大小为![]() .
.
(Ⅲ)![]() 中,
中,![]() ,
,![]() .
.
在正三棱柱中,![]() 到平面
到平面![]() 的距离为
的距离为![]() .设点
.设点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
由![]() 得
得![]() ,
,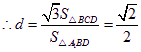 .
.
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
解法二:(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() 为正三角形,
为正三角形,![]() .
.
![]() 在正三棱柱
在正三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
取![]() 中点
中点![]() ,以
,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,

![]() ,
,![]() .
.
![]() 平面
平面![]() .
.
(Ⅱ)设平面![]() 的法向量为
的法向量为![]() .
.
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
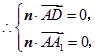
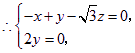
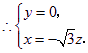
令![]() 得
得![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
由(Ⅰ)知![]() 平面
平面![]() ,
,![]() 为平面
为平面![]() 的法向量.
的法向量.
![]() ,
,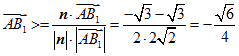 .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
(Ⅲ)由(Ⅱ),![]() 为平面
为平面![]() 法向量,
法向量,
![]() .
.
![]() 点
点![]() 到平面
到平面![]() 的距离
的距离 .
.

练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面