题目内容
设函数 在
在 时取得极值.
时取得极值.
(1)求 的值;
的值;
(2)求函数 的单调区间.
的单调区间.
(1) ;(2)
;(2) 的单调递增区间为
的单调递增区间为 ;单调递减区间为
;单调递减区间为 .
.
【解析】
试题分析:(1)因为函数 在
在 取得极值,所以:
取得极值,所以: ,得到关于
,得到关于 的方程,求得
的方程,求得 ;(2)由(1)知
;(2)由(1)知 ,定义域为
,定义域为 ,对其求导得到:
,对其求导得到: ,令导函数
,令导函数 ,令
,令 ,分别求得原函数的单调递增区间和单调递减区间.
,分别求得原函数的单调递增区间和单调递减区间.
试题解析:(1) 当
当 时取极值,则
时取极值,则
解得: .
.
(2)
令 解得:
解得: 令
令 解得:
解得:
所以 的单调递增区间为
的单调递增区间为 ;单调递减区间为
;单调递减区间为 .
.
考点:1.函数的极值;2.函数的单调性.

练习册系列答案
相关题目
 ⊥平面
⊥平面 ,
,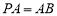 ,
,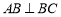 ,
,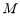 为
为 中点.
中点.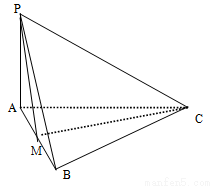
 ;
;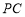 与平面
与平面 所成角的正切值 为
所成角的正切值 为 ,求二面角
,求二面角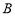 -
- -
- 的正弦值.
的正弦值.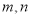 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,给出下列命题,正确的是( )
是三个不同的平面,给出下列命题,正确的是( )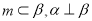 ,则
,则
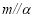 ,
, ,则
,则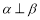
 ,
, ,则
,则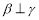
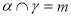 ,
, ,
,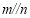 ,则
,则 [
[ ,则
,则 ”的否命题为“若
”的否命题为“若 ,则
,则 ”
” ,
, ”的否定是“存在
”的否定是“存在 ,
, ”;
”; ”是“
”是“ ”的充要条件;
”的充要条件; 所表示的圆有最大面积,则取最大面积时,该圆的圆心坐标为( )
所表示的圆有最大面积,则取最大面积时,该圆的圆心坐标为( ) 的导函数
的导函数 的图象,给出下列命题
的图象,给出下列命题
 是函数
是函数 的极值点.
的极值点. 是函数
是函数 的极小值点.
的极小值点. 在
在 处切线斜率大于
处切线斜率大于 .
. 在区间
在区间 上单调递减.则正确命题的序号是 .
上单调递减.则正确命题的序号是 .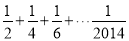 的值的程序框图,其中判断框内应填入的是( ).
的值的程序框图,其中判断框内应填入的是( ).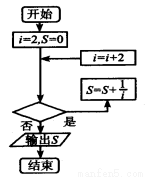
 B.
B.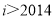 C.
C.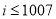 D.
D.
 极大值为 .
极大值为 .