Question

已知函数y=3sin(x-).

(1)用“五点法”作函数的图象；

(2)求函数的周期；

(3)求函数的单调递增区间；

(4)求此函数的对称轴、对称中心.

Answer 1

解：(1)

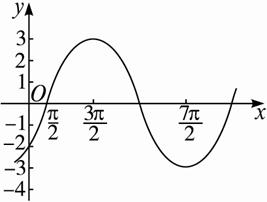
(2)因为3sin［(x+4π)-］=3sin(x-+2π)=3sin(x-)，所以由周期函数的定义，知原函数的周期是4π；也可以直接用公式：T===4π.

(3)x前的系数为正数，所以把x-视为一个整体，令-+2kπ≤x-≤+2kπ，解得［-+4kπ，+4kπ］，k∈Z，即为函数的单调递增区间.

(4)由于y=3sin(x-)是周期函数，通过观察图象可知所有与x轴垂直并且通过图象的最值点的直线都是此函数的对称轴，即令x-=+kπ，解得直线方程为x=+2kπ，k∈Z.

图象与x轴的所有交点都是函数的对称中心，所以对称中心为点(+2kπ，0)，k∈Z.