Question

如图所示，我校计划在汉东中学操场北修建一个矩形花坛并在花坛内装置两个相同的喷水器．已知喷水器的喷水区域是半径为5m的圆．问如何设计花坛的尺寸和两个喷水器的位置，才能使花坛的面积最大且能全部喷到水？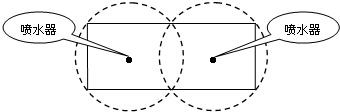

Answer 1

设花坛的长、宽分别为xm，ym，根据要求，矩形花坛应在喷水区域内，顶点应恰好位于喷水区域的边界．
依题意得：(

x

4

)2+(

y

2

)2=25，（x＞0，y＞0）
问题转化为在x＞0，y＞0，

x2

4

+y2=100的条件下，求S=xy的最大值．
∵S=xy=2?

x

2

?y≤(

x

2

)2+y2=100，
由

x

2

=y和

x2

4

+y2=100及x＞0，y＞0得：x=10

2

，y=5

2

∴S_max=100
答：花坛的长为10

2

m，宽为5

2

m，两喷水器位于矩形分成的两个正方形的中心，则符合要求．