题目内容
变量U与V相对应的一组样本数据为（1，1.4），（2，2.2），（3，3），（4，3.8），由上述样本数据得到U与V的线性回归分析，R2表示解释变量对于预报变量变化的贡献率，则R2=（ ）A．
B．
C．1
D．3
【答案】分析：由给出的两个变量呈线性相关，所以相关指数就等于相关系数，直接代入相关系数公式求解即可．
解答：解：在线性回归中，相关指数R2等于相关系数，
由x1=1，x2=2，x3=3，x4=4得：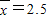
，
y1=1.4，y2=2.2，y3=3，y4=3.8得：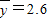
，
所以相关系数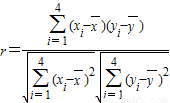
=
=
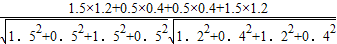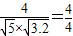=1．
故选C．
点评：本题考查了相关系数，考查了学生的计算能力，考查了对公式的记忆，解答此题的关键是懂得呈线性相关的两个变量的相关指数就等于相关系数，此题是基础题．
解答：解：在线性回归中，相关指数R2等于相关系数，
由x1=1，x2=2，x3=3，x4=4得：
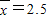，y1=1.4，y2=2.2，y3=3，y4=3.8得：
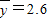，所以相关系数
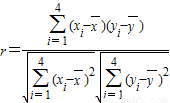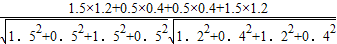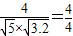===1．故选C．
点评：本题考查了相关系数，考查了学生的计算能力，考查了对公式的记忆，解答此题的关键是懂得呈线性相关的两个变量的相关指数就等于相关系数，此题是基础题．
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
变量X与Y相对应的一组数据为（10，1），（11.3，2），（11.8，3），（12.5，4），（13，5），变量U与V相对应的一组数据为 （10，5），（11.3，4），（11.8，3），（12.5，2），（13，1）．r1表示变量Y与X之间的线性相关系数，r2表示变量V与U之间的线性相关系数，则（ ）
| A、r2＜r1＜0 | B、0＜r2＜r1 | C、r2＜0＜r1 | D、r2=r1 |
| 下列命题： ①设函数f（x）=g（x）+x2，曲线y=g（x）在点（1，g（1））处的切线方程为y=2x+1，则曲线y=f（x）在点（1，f（1））处切线的斜率为-
②关于x的不等式（a-3）x2＜（4a-2）x对任意的a∈（0，1）恒成立，则x的取值范围是(-∞，-1]∪[
③变量X与Y相对应的一组数据为（10，1），（11.3，2），（11.8，3），（12.5，4），（13，5）；变量U与V相对应的一组数据为（10，5），（11.3，4），（11.8，3），（12.5，2），（13，1），r1表示变量Y与X之间的线性相关系数，r2表示变量V与U之间的线性相关系数，则r2＜0＜r1； ④下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对照数据
以上命题正确的个数是（ ） |
表示变量Y与X之间的线性相关系数,
表示变量V与U之间的线性相关系数,则 ( )
B. 
C.
D. 