题目内容
已知点G为△ABC的重心,过点G作直线与AB、AC两边分别交于M、N两点,且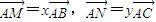 ,求
,求 +
+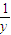 的值.
的值.
【答案】分析:由G为三角形的重心则 =
= (
( +
+ ),结合
),结合 ,我们根据M,G,N三点共线,易得到x,y的关系式,整理后即可得到
,我们根据M,G,N三点共线,易得到x,y的关系式,整理后即可得到 +
+ 的值.
的值.
解答:解:根据题意G为三角形的重心,
 =
= (
( +
+ ),
),
 =
= -
- =
= (
( +
+ )-x
)-x =
= ,
,

=
= ,
,
由于 与
与 共线,根据共线向量基本定理知,存在实数λ,使得
共线,根据共线向量基本定理知,存在实数λ,使得 ,
,
即
 +
+
 =
= ,
,
即
∴
即x+y-3xy=0
两边同除以xy整理得 +
+ =3.
=3.
点评:本题考查的知识点是向量的线性运算性质及几何意义,向量的共线定理,及三角形的重心,其中根据 与
与 共线,根据共线向量基本定理知,存在实数λ,使得
共线,根据共线向量基本定理知,存在实数λ,使得 ,进而得到x,y的关系式,是解答本题的关键.
,进而得到x,y的关系式,是解答本题的关键.
 =
= (
( +
+ ),结合
),结合 ,我们根据M,G,N三点共线,易得到x,y的关系式,整理后即可得到
,我们根据M,G,N三点共线,易得到x,y的关系式,整理后即可得到 +
+ 的值.
的值.解答:解:根据题意G为三角形的重心,
 =
= (
( +
+ ),
), =
= -
- =
= (
( +
+ )-x
)-x =
= ,
,
=

=
 ,
,由于
 与
与 共线,根据共线向量基本定理知,存在实数λ,使得
共线,根据共线向量基本定理知,存在实数λ,使得 ,
,即

 +
+
 =
= ,
,即

∴

即x+y-3xy=0
两边同除以xy整理得
 +
+ =3.
=3.点评:本题考查的知识点是向量的线性运算性质及几何意义,向量的共线定理,及三角形的重心,其中根据
 与
与 共线,根据共线向量基本定理知,存在实数λ,使得
共线,根据共线向量基本定理知,存在实数λ,使得 ,进而得到x,y的关系式,是解答本题的关键.
,进而得到x,y的关系式,是解答本题的关键. 
练习册系列答案
相关题目