题目内容

已知12＜m＜60，15＜n＜36，则
m
n
的取值范围是
（
1
3
，4）
（
1
3
，4）
．
分析：根据不等式的性质进行求解范围即可．
解答：解：∵15＜n＜36，
∴
1
36
＜
1
n
＜
1
15
，
∵12＜m＜60，
∴12×
1
36
＜
m
n
＜60×
1
15
，即
1
3
＜
m
n
＜4，
∴
m
n
的取值范围是（
1
3
，4）．
点评：本题主要考查不等式的应用，利用不等式的性质可以求变量的取值范围．
练习册系列答案
相关题目
已知椭圆C的两个焦点为F1(-2
2
，0)，F2(2
2
，0)，P为椭圆上一点，满足∠F1PF2=60°．
（1）当直线l过F1与椭圆C交于M、N两点，且△MF2N的周长为12时，求C的方程；
（2）求△F1PF2的面积．
已知抛物线y2=4x的焦点为F，准线与x轴的交点为M，N为抛物线上的一点，且|NF|=
1
2
|MN|，则∠NMF=（　　）
A、45°B、30°
C、75°D、60°
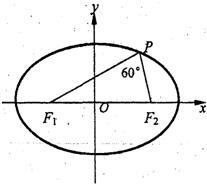精英家教网已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右焦点分别为F1、F2，P是椭圆上一点，且∠F1PF2=60°，设
|PF1|
|PF2|
=λ
（1）求椭圆C的离心率e和λ的函数关系式e=f（λ）
（2）若椭圆C的离心率e最小，且椭圆C上的动点M到定点N(0，
1
2
)的最远距离为
5
，求椭圆C的方程．
在平等四边形ABCD中，已知AB=2，AD=1，∠DAB=60°，点M为AB的中点，点P在BC（包括端点），则
AP
•
DM
的取值范围是
[
1
2
，1]
[
1
2
，1]
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网