题目内容
设
(1)求f(x)= 的表达式
的表达式
(2)求f(x) 的单调区间
(3)求f(x)的最大值和最小值.

(1)求f(x)=
 的表达式
的表达式(2)求f(x) 的单调区间
(3)求f(x)的最大值和最小值.
解:(1)∵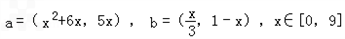 ,
,
∴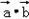 =(x2+6x,5x)
=(x2+6x,5x)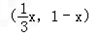 =
=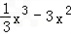 +5x,
+5x,
∴f(x)=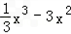 +5x,x∈[0,9].
+5x,x∈[0,9].
(2)∵f(x)=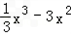 +5x,x∈[0,9],
+5x,x∈[0,9],
∴f'(x)=x2﹣6x+5,
令f'(x)=0,得x=1,或x=5,
由f'(x)=x2﹣6x+5>0,得x>5,或x<1.
由f'(x)=x2﹣6x+5<0,得1<x<5.
∴f(x)在[0,1)上单调递增,在(1,5)上单调递减,在(5,9]上单调递增.
(3)∵f(0)=0,f(1)= ,f(5)=﹣
,f(5)=﹣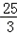 ,f(9)=45,
,f(9)=45,
∴f(x)的最大值是45,最小值是﹣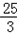 .
.
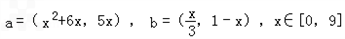 ,
,∴
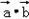 =(x2+6x,5x)
=(x2+6x,5x)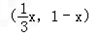 =
=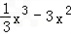 +5x,
+5x,∴f(x)=
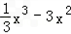 +5x,x∈[0,9].
+5x,x∈[0,9].(2)∵f(x)=
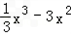 +5x,x∈[0,9],
+5x,x∈[0,9],∴f'(x)=x2﹣6x+5,
令f'(x)=0,得x=1,或x=5,
由f'(x)=x2﹣6x+5>0,得x>5,或x<1.
由f'(x)=x2﹣6x+5<0,得1<x<5.
∴f(x)在[0,1)上单调递增,在(1,5)上单调递减,在(5,9]上单调递增.
(3)∵f(0)=0,f(1)=
 ,f(5)=﹣
,f(5)=﹣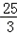 ,f(9)=45,
,f(9)=45,∴f(x)的最大值是45,最小值是﹣
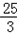 .
.
练习册系列答案
相关题目
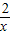 +1-a1nx(a>0).
+1-a1nx(a>0).