题目内容
已知α为第二象限角,cos| α |
| 2 |
| α |
| 2 |
| ||
| 2 |
| α |
| 2 |
| α |
| 2 |
分析:本题考查的知识是同角三角函数基本关系的运用,及倍角公式,由已知中知α为第二象限角,且cos
+sin
=-
,平方后,我们易得sinα值,进而也可给出cosα,利用平方差公式,即可求出sin
-cos
,利用倍角公式即可求出sin2α+cos2α的值
| α |
| 2 |
| α |
| 2 |
| ||
| 2 |
| α |
| 2 |
| α |
| 2 |
解答:解:由cos
+sin
=-
平方得
1+2sin
cos
=
,
即sinα=
,cosα=-
.
此时kπ+
<
<kπ+
.
∵cos
+sin
=-
<0,
sin
cos
=
>0,
∴cos
<0,sin
<0.
∴
为第三象限角.
∴2kπ+
<
<2kπ+
,k∈Z.
∴sin
<cos
,
即sin
-cos
<0.
∴sin
-cos
=-
=-
,
sin2α+cos2α=2sinαcosα+1-2sin2α=
.
| α |
| 2 |
| α |
| 2 |
| ||
| 2 |
1+2sin
| α |
| 2 |
| α |
| 2 |
| 5 |
| 4 |
即sinα=
| 1 |
| 4 |
| ||
| 4 |
此时kπ+
| π |
| 4 |
| α |
| 2 |
| π |
| 2 |
∵cos
| α |
| 2 |
| α |
| 2 |
| ||
| 2 |
sin
| α |
| 2 |
| α |
| 2 |
| 1 |
| 8 |
∴cos
| α |
| 2 |
| α |
| 2 |
∴
| α |
| 2 |
∴2kπ+
| 5π |
| 4 |
| α |
| 2 |
| 3π |
| 2 |
∴sin
| α |
| 2 |
| α |
| 2 |
即sin
| α |
| 2 |
| α |
| 2 |
∴sin
| α |
| 2 |
| α |
| 2 |
| 1-sinα |
| ||
| 2 |
sin2α+cos2α=2sinαcosα+1-2sin2α=
7-
| ||
| 8 |
点评:三角函数给值求值问题的关键就是分析已知角与未知角的关系,然后通过角的关系,选择恰当的公式,即:如果角与角相等,则使用同角三角函数关系;如果角与角之间的和或差是直角的整数倍,则使用诱导公式;如果角与角之间存在和差关系,则我们用和差角公式;如果角与角存在倍数关系,则使用倍角公式.由三角函数值判断
的范围是关键.
| α |
| 2 |

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 ,则2a是( )
,则2a是( ) ,
, 为第二象限角,求
为第二象限角,求 ;
; ,求
,求 的值。
的值。 ,
, 为第二象限角,求
为第二象限角,求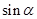 和
和 及
及 的值.
的值.