题目内容
非零向量 使得
使得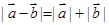 成立的一个充分非必要条件是( )
成立的一个充分非必要条件是( )
A.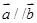 | B.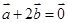 | C.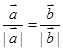 | D.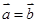 |
B
解析试题分析:根据题意,等式表示的为差向量的模等于两个非零向量的模的差,那么可知只有共线且方向的时候能成立,因此可知其充要条件是共线且方向。那么它成立的一个充分不必要条件是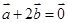 ,其余的都是非充分非必要条件,故选B.
,其余的都是非充分非必要条件,故选B.
考点:向量的加法的几何意义
点评:熟练的求解出非零向量 使得
使得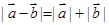 成立的一个充要条件是关键,属于基础题
成立的一个充要条件是关键,属于基础题

练习册系列答案
相关题目
向量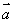 与
与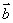 的夹角为
的夹角为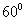 ,
,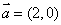 ,
,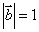 则
则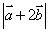 =( )
=( )
A.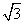 | B.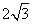 | C.4 | D.12 |
已知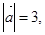
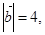
 则
则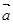 与
与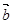 的夹角为 ( )
的夹角为 ( )
A.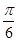 | B.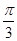 | C.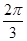 | D. |
已知平面上不共线的四点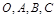 ,若
,若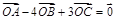 ,则
,则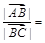
| A.3 | B.4 | C.5 | D.6 |
下列命题:①在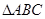 中,若
中,若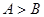 ,则
,则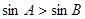 ;②已知
;②已知 ,则
,则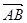 在
在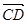 上的投影为
上的投影为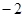 ;③已知
;③已知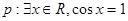 ,
,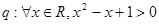 ,则“
,则“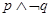 ”为假命题.其中真命题的个数为( )
”为假命题.其中真命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
在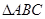 中,
中,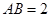 ,
,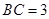 ,
,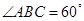 ,
,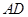 为
为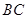 边上的高,
边上的高, 为
为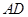 的中点,若
的中点,若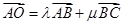 ,则
,则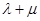 的值为()
的值为()
A.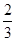 | B.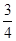 | C.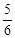 | D.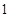 |
设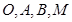 为平面上四点,
为平面上四点,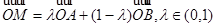 ,则
,则
A.点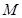 在线段 在线段 上 上 | B.点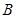 在线段 在线段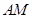 上 上 |
C.点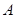 在线段 在线段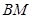 上 上 | D.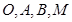 四点共线 四点共线 |
设 =(2
=(2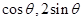 ),
),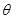
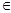 (
(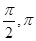 );
); =(0,-1),则
=(0,-1),则 与
与 夹角为
夹角为
A.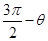 | B.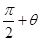 | C.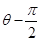 | D.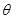 |
已知平面上三点A,B,C满足 ,则△ABC的形状是( )
,则△ABC的形状是( )
| A.等腰三角形 | B.等边三角形 |
| C.直角三角形 | D.等腰直角三角形 |