题目内容
已知动圆过定点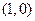 ,且与直线
,且与直线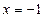 相切.
相切.
(1)求动圆的圆心轨迹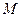 的方程;
的方程;
(2) 是否存在直线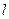 ,使
,使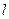 过点
过点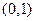 ,并与轨迹
,并与轨迹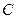 交于
交于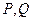 两点,且满足
两点,且满足
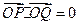 ?若存在,求出直线
?若存在,求出直线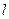 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
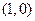 ,且与直线
,且与直线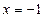 相切.
相切.(1)求动圆的圆心轨迹
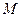 的方程;
的方程;(2) 是否存在直线
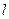 ,使
,使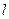 过点
过点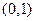 ,并与轨迹
,并与轨迹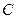 交于
交于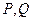 两点,且满足
两点,且满足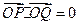 ?若存在,求出直线
?若存在,求出直线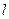 的方程;若不存在,说明理由.
的方程;若不存在,说明理由. (1)动点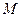 的轨迹方程为
的轨迹方程为 ;(2) 直线
;(2) 直线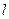 存在,其方程为
存在,其方程为 .
.
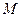 的轨迹方程为
的轨迹方程为 ;(2) 直线
;(2) 直线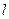 存在,其方程为
存在,其方程为 .
.
(1)如图,设
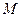 为动圆圆心,
为动圆圆心,  ,过点
,过点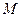 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,由题意知:
,由题意知: ,
, 即动点
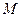 到定点
到定点 与定直线
与定直线 的距离相等,由抛物线 的定义知,点
的距离相等,由抛物线 的定义知,点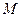 的轨迹为抛物线,其中
的轨迹为抛物线,其中 为焦点,
为焦点, 为准线, ∴ 动点
为准线, ∴ 动点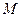 的轨迹方程为
的轨迹方程为 ;
; (2)由题可设直线
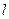 的方程为
的方程为 ,
,由
 得
得
△
 ,
, ,
, 设
 ,
, ,则
,则 ,
, ,
, 由
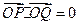 ,即
,即  ,
, ,于是
,于是 ,
, 即
 ,
, ,
, ,解得
,解得 或
或 (舍去),
(舍去),又
 ,
, ∴ 直线
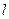 存在,其方程为
存在,其方程为 .
.
练习册系列答案
相关题目
 椭圆方程为
椭圆方程为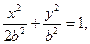 抛物线方程为
抛物线方程为 如图4所示,过点
如图4所示,过点 作
作 轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
轴的平行线,与抛物线在第一象限的交点为G.已知抛物线在点G的切线经过椭圆的右焦点
 为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标) 。
为直角三角形?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标) 。
 -
- =1的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r= ( )
=1的渐近线与圆(x-3)2+y2=r2(r>0)相切,则r= ( )

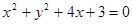 与抛物线
与抛物线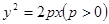 的准线相切,则
的准线相切,则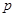 = .
= .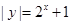 与直线
与直线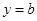 没有公共点,则
没有公共点,则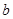 的取值范围是________________.
的取值范围是________________.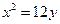 的切线垂直于直线
的切线垂直于直线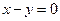 ,则切线方程为 .
,则切线方程为 .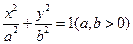 的焦点坐
的焦点坐 标为
标为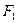 (
(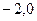 ),点M(
),点M(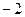 ,
,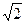 )在椭圆E上
)在椭圆E上 (1)求椭圆E的方程;(2)O为坐标原点,⊙
(1)求椭圆E的方程;(2)O为坐标原点,⊙ 的任意一条切线与椭圆E有两个交点
的任意一条切线与椭圆E有两个交点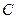 ,
,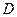 且
且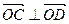 ,求⊙
,求⊙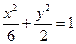 的焦点,P是曲线
的焦点,P是曲线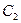 :
: 与C1的一个交点,
与C1的一个交点,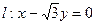 与曲线
与曲线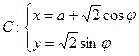
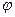 为参数,
为参数,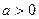 )有两个公共点A,B,且|AB|=2,则实数a的值为 ;在此条件下,以直角坐标系的原点为极点,x轴正方向为极轴建立坐标系,则曲线C的极坐标方程为 .
)有两个公共点A,B,且|AB|=2,则实数a的值为 ;在此条件下,以直角坐标系的原点为极点,x轴正方向为极轴建立坐标系,则曲线C的极坐标方程为 .