题目内容
已知锐角三角形ABC三个内角分别为A、B、C，向量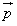
=（2-2sinA，cosA+sinA）与向量
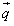=（sinA-cosA，1+sinA）是共线向量．
（I）求∠A的值；
（Ⅱ）求函数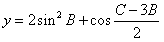
的值域．
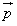=（2-2sinA，cosA+sinA）与向量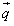=（sinA-cosA，1+sinA）是共线向量．（I）求∠A的值；
（Ⅱ）求函数
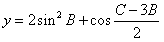的值域． 解：（Ⅰ）
∴(2-2sin A)(1+sin A)=(cos A+sin A)(sin A-cos A)，
∴sin2A=
，
又△ABC为锐角三角形，
∴sinA=
，∴A=
。
（2）
，
∵B∈(0，
)，又因为B+A＞
，
∴
＜B＜
，
∴
，∴y∈
。
∴(2-2sin A)(1+sin A)=(cos A+sin A)(sin A-cos A)，
∴sin2A=
，又△ABC为锐角三角形，
∴sinA=
，∴A=。 （2）
，∵B∈(0，
)，又因为B+A＞，∴
＜B＜，∴
，∴y∈。 
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目