题目内容
当 时,函数y=ax+b和f(x)在同一坐标系内的大致图象是
时,函数y=ax+b和f(x)在同一坐标系内的大致图象是
- A.

- B.

- C.

- D.

A
分析:由给出的指数函数可以断定a与b同号,依此可以排除选项C、D,再根据A、B中指数函数的图象都是单调递减,断定0<b<a,由此说明直线y=ax+b在y轴上的绝对值应小于直线在x轴上的绝对值,则正确答案可求.
解答:由 知,
知, ,且
,且 .
.
说明a,b同号且不相等,
若a<0,则b<0,所以选项C和D的直线不符合,
若a>0,则b>0,仅由此看,选项A、B中的直线似乎都可以,
但由指数函数的图象看出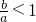 ,所以直线y=ax+b在y轴上的绝对值应小于直线在x轴上的绝对值,
,所以直线y=ax+b在y轴上的绝对值应小于直线在x轴上的绝对值,
因此只有选项A符合.
故选A.
点评:本题考查了函数的图象,解答此题的关键是正确分析出实数a,b的符号及大小关系,是基础题.
分析:由给出的指数函数可以断定a与b同号,依此可以排除选项C、D,再根据A、B中指数函数的图象都是单调递减,断定0<b<a,由此说明直线y=ax+b在y轴上的绝对值应小于直线在x轴上的绝对值,则正确答案可求.
解答:由
 知,
知, ,且
,且 .
.说明a,b同号且不相等,
若a<0,则b<0,所以选项C和D的直线不符合,
若a>0,则b>0,仅由此看,选项A、B中的直线似乎都可以,
但由指数函数的图象看出
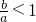 ,所以直线y=ax+b在y轴上的绝对值应小于直线在x轴上的绝对值,
,所以直线y=ax+b在y轴上的绝对值应小于直线在x轴上的绝对值,因此只有选项A符合.
故选A.
点评:本题考查了函数的图象,解答此题的关键是正确分析出实数a,b的符号及大小关系,是基础题.

练习册系列答案
相关题目
 时,函数y=ax+b和f(x)在同一坐标系内的大致图象是( )
时,函数y=ax+b和f(x)在同一坐标系内的大致图象是( )



 时,函数
时,函数 恒成立,如果p∨q为真命题,p∧q为假命题,求a的取值范围.
恒成立,如果p∨q为真命题,p∧q为假命题,求a的取值范围.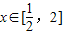 时,函数
时,函数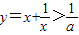 恒成立,如果p∨q为真命题,p∧q为假命题,求a的取值范围.
恒成立,如果p∨q为真命题,p∧q为假命题,求a的取值范围. ;
; 时,问△OPnQn的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
时,问△OPnQn的面积是否存在最大值?若存在,求出最大值;若不存在,请说明理由.