题目内容
已知a>0,设命题p:函数y=ax为减函数;命题q:当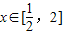 时,函数
时,函数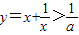 恒成立,如果p∨q为真命题,p∧q为假命题,求a的取值范围.
恒成立,如果p∨q为真命题,p∧q为假命题,求a的取值范围.
【答案】分析:由题意得函数y=ax为减函数所以0<a<1,当 时函数
时函数 恒成立则a>
恒成立则a> ,因为p∨q为真命题,p∧q为假命题所以命题p与命题q一个是真一个是假,所以a的范围是0<a
,因为p∨q为真命题,p∧q为假命题所以命题p与命题q一个是真一个是假,所以a的范围是0<a 或a≥1.
或a≥1.
解答:解:由题意得
∵函数y=ax为减函数
∴0<a<1
∵函数
∴函数的值域为[2,2.5]
∵函数 恒成立
恒成立
∴ymin>
∴a>
∵p∨q为真命题,p∧q为假命题
∴命题p与命题q一个是真一个是假
∴0<a 或a≥1
或a≥1
所以a的取值范围为 .
.
故答案为 .
.
点评:解决此类问题的方法是先假设简单命题为真时求出参数的范围然后根据复合命题的真假得出结论,最后用集合的知识取交集取并集.
 时函数
时函数 恒成立则a>
恒成立则a> ,因为p∨q为真命题,p∧q为假命题所以命题p与命题q一个是真一个是假,所以a的范围是0<a
,因为p∨q为真命题,p∧q为假命题所以命题p与命题q一个是真一个是假,所以a的范围是0<a 或a≥1.
或a≥1.解答:解:由题意得
∵函数y=ax为减函数
∴0<a<1
∵函数

∴函数的值域为[2,2.5]
∵函数
 恒成立
恒成立∴ymin>

∴a>

∵p∨q为真命题,p∧q为假命题
∴命题p与命题q一个是真一个是假
∴0<a
 或a≥1
或a≥1所以a的取值范围为
 .
.故答案为
 .
.点评:解决此类问题的方法是先假设简单命题为真时求出参数的范围然后根据复合命题的真假得出结论,最后用集合的知识取交集取并集.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目