题目内容
已知抛物线x2=4y的焦点为F,过F任作直线l(l与x轴不平行)交抛物线分别于A,B两点,点A关于y轴对称点为C,(1)求证:直线BC与y轴交点D必为定点;
(2)过A,B分别作抛物线的切线,两条切线交于E,求
 的最小值,并求当
的最小值,并求当 取最小值时直线l的方程.
取最小值时直线l的方程.
【答案】分析:(1)设出直线l的方程,和抛物线方程联立后得到关于x的一元二次方程,利用根与系数关系得到两个交点A,B的横坐标的和与积,由对称性得到A关于y轴的对称点C,写出直线BC的方程后由线系方程可证过定点;
(2)求出函数的导函数,写出过A,B的切线方程,把两切线方程分别作差和作和后求出两切线焦点的纵坐标,则|DE|可求,由弦长公式求出|AB|,作比后利用基本不等式求最值,并求出 取最小值时直线l的方程.
取最小值时直线l的方程.
解答: (1)证明:设A(x1,y1),B(x2,y2),
(1)证明:设A(x1,y1),B(x2,y2),
∵抛物线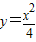 的焦点为F(0,1),
的焦点为F(0,1),
∴可设直线l的方程为:y=kx+1(k≠0).
联立 ,消去y并整理得:x2-4kx-4=0
,消去y并整理得:x2-4kx-4=0
所以x1+x2=4k,x1x2=-4
由对称性知C(-x1,y1),
直线BC的方程为 ,即
,即
∴直线BC与y轴交于定点D(0,-1)
(2) ,∴过点A的切线方程为:
,∴过点A的切线方程为: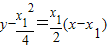
即: ①,同理可得过点B的切线方程为:
①,同理可得过点B的切线方程为:
 ②
②
①-②得: (x1≠x2)
(x1≠x2)
∴
①+②得:

=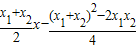
= .
.
∴y=-1.
∴E(2k,-1),|DE|=2|k|


∴ ,取等号时,k=±1,
,取等号时,k=±1,
直线l的方程为:y=x+1或y=-x+1.
点评:本题主要考查抛物线的定义和直线与曲线的相切问题,解决此类问题的必须熟悉曲线的定义和曲线的图形特征,考查抛物线的应用,关键是看清题中给出的条件,灵活运用韦达定理,中点坐标公式进行求解.这也是高考常考的知识点,该题是难题.
(2)求出函数的导函数,写出过A,B的切线方程,把两切线方程分别作差和作和后求出两切线焦点的纵坐标,则|DE|可求,由弦长公式求出|AB|,作比后利用基本不等式求最值,并求出
 取最小值时直线l的方程.
取最小值时直线l的方程.解答:
 (1)证明:设A(x1,y1),B(x2,y2),
(1)证明:设A(x1,y1),B(x2,y2),∵抛物线
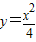 的焦点为F(0,1),
的焦点为F(0,1),∴可设直线l的方程为:y=kx+1(k≠0).
联立
 ,消去y并整理得:x2-4kx-4=0
,消去y并整理得:x2-4kx-4=0所以x1+x2=4k,x1x2=-4
由对称性知C(-x1,y1),

直线BC的方程为
 ,即
,即
∴直线BC与y轴交于定点D(0,-1)
(2)
 ,∴过点A的切线方程为:
,∴过点A的切线方程为: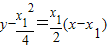
即:
 ①,同理可得过点B的切线方程为:
①,同理可得过点B的切线方程为: ②
②①-②得:
 (x1≠x2)
(x1≠x2)∴

①+②得:


=
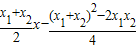
=
 .
.∴y=-1.
∴E(2k,-1),|DE|=2|k|


∴
 ,取等号时,k=±1,
,取等号时,k=±1,直线l的方程为:y=x+1或y=-x+1.
点评:本题主要考查抛物线的定义和直线与曲线的相切问题,解决此类问题的必须熟悉曲线的定义和曲线的图形特征,考查抛物线的应用,关键是看清题中给出的条件,灵活运用韦达定理,中点坐标公式进行求解.这也是高考常考的知识点,该题是难题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 已知抛物线x2=4y上的点P(非原点)处的切线与x轴,y轴分别交于Q,R两点,F为焦点.
已知抛物线x2=4y上的点P(非原点)处的切线与x轴,y轴分别交于Q,R两点,F为焦点. (2009•温州一模)如图,已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于D,并交l于点E,过H作直线HF垂直直线l,并交x轴于点F.
(2009•温州一模)如图,已知抛物线x2=4y,过抛物线上一点A(x1,y1)(不同于顶点)作抛物线的切线l,并交x轴于点C,在直线y=-1上任取一点H,过H作HD垂直x轴于D,并交l于点E,过H作直线HF垂直直线l,并交x轴于点F. (2011•浙江模拟)已知抛物线x2=4y,圆C:x2+(y-2)2=4,M(x0,y0),(x0>0,y0>0)为抛物线上的动点.
(2011•浙江模拟)已知抛物线x2=4y,圆C:x2+(y-2)2=4,M(x0,y0),(x0>0,y0>0)为抛物线上的动点.