题目内容
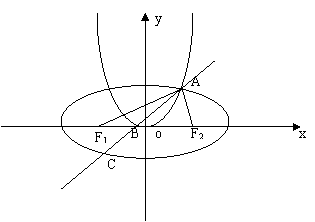
实轴长为 的椭圆的中心在原点,其焦点F1,,F2在x轴上.抛物线的顶点在原点O,对称轴为y轴,两曲线在第一象限内相交于点A,且AF1⊥AF2,△AF1F2的面积为3.
的椭圆的中心在原点,其焦点F1,,F2在x轴上.抛物线的顶点在原点O,对称轴为y轴,两曲线在第一象限内相交于点A,且AF1⊥AF2,△AF1F2的面积为3.(Ⅰ)求椭圆和抛物线的标准方程;
(Ⅱ)过点A作直线l分别与抛物线和椭圆交于B,C,若
 ,求直线l的斜率k.
,求直线l的斜率k.
【答案】分析:(Ⅰ)设椭圆方程为 ,AF1=m,AF2=n,由题意知
,AF1=m,AF2=n,由题意知 ,由此能求出椭圆的方程和抛物线方程.
,由此能求出椭圆的方程和抛物线方程.
(Ⅱ)设直线l的方程为 ,B(x1,y1),C(x2,y2).由
,B(x1,y1),C(x2,y2).由 ,得
,得 ,联立直线与抛物线的方程
,联立直线与抛物线的方程 ,得
,得 ,
, .联立直线与椭圆的方程
.联立直线与椭圆的方程 ,得
,得 .由此能求出直线l的斜率.
.由此能求出直线l的斜率.
解答:解:(Ⅰ)设椭圆方程为 ,AF1=m,AF2=n
,AF1=m,AF2=n
由题意知 …(2分)
…(2分)
解得c2=9,∴b2=12-9=3.
∴椭圆的方程为 …(4分)
…(4分)
∵yA×c=3,∴yA=1,代入椭圆的方程得 ,
,
将点A坐标代入得抛物线方程为x2=8y. …(6分)
(Ⅱ)设直线l的方程为 ,B(x1,y1),C(x2,y2)
,B(x1,y1),C(x2,y2)
由 得
得 ,
,
化简得 …(8分)
…(8分)
联立直线与抛物线的方程 ,
,
得
∴ ①…(10分)
①…(10分)
联立直线与椭圆的方程
得
∴ ②…(12分)
②…(12分)
∴
整理得: ∴
∴ ,所以直线l的斜率为
,所以直线l的斜率为 . …(14分)
. …(14分)
点评:本题考查椭圆和抛物线的标准方程的求法和求直线l的斜率k.解题时要认真审题,注意挖掘题设中的隐含条件,灵活运用椭圆性质,合理地进行等价转化.
 ,AF1=m,AF2=n,由题意知
,AF1=m,AF2=n,由题意知 ,由此能求出椭圆的方程和抛物线方程.
,由此能求出椭圆的方程和抛物线方程.(Ⅱ)设直线l的方程为
 ,B(x1,y1),C(x2,y2).由
,B(x1,y1),C(x2,y2).由 ,得
,得 ,联立直线与抛物线的方程
,联立直线与抛物线的方程 ,得
,得 ,
, .联立直线与椭圆的方程
.联立直线与椭圆的方程 ,得
,得 .由此能求出直线l的斜率.
.由此能求出直线l的斜率.解答:解:(Ⅰ)设椭圆方程为
 ,AF1=m,AF2=n
,AF1=m,AF2=n由题意知
 …(2分)
…(2分)解得c2=9,∴b2=12-9=3.
∴椭圆的方程为
 …(4分)
…(4分)∵yA×c=3,∴yA=1,代入椭圆的方程得
 ,
,将点A坐标代入得抛物线方程为x2=8y. …(6分)
(Ⅱ)设直线l的方程为
 ,B(x1,y1),C(x2,y2)
,B(x1,y1),C(x2,y2)由
 得
得 ,
,化简得
 …(8分)
…(8分)联立直线与抛物线的方程
 ,
,得

∴
 ①…(10分)
①…(10分)联立直线与椭圆的方程

得

∴
 ②…(12分)
②…(12分)∴

整理得:
 ∴
∴ ,所以直线l的斜率为
,所以直线l的斜率为 . …(14分)
. …(14分)点评:本题考查椭圆和抛物线的标准方程的求法和求直线l的斜率k.解题时要认真审题,注意挖掘题设中的隐含条件,灵活运用椭圆性质,合理地进行等价转化.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 实轴长为
实轴长为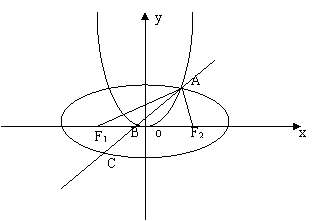 (Ⅱ)过点
(Ⅱ)过点 的椭圆的中心在原点,其焦点F1,,F2在x轴上.抛物线的顶点在原点O,对称轴为y轴,两曲线在第一象限内相交于点A,且AF1⊥AF2,△AF1F2的面积为3.
的椭圆的中心在原点,其焦点F1,,F2在x轴上.抛物线的顶点在原点O,对称轴为y轴,两曲线在第一象限内相交于点A,且AF1⊥AF2,△AF1F2的面积为3. ,求直线l的斜率k.
,求直线l的斜率k.