题目内容
已知椭圆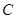 的中心为坐标原点
的中心为坐标原点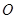 ,一个长轴端点为
,一个长轴端点为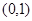 ,短轴端点和焦点所组成的四边形为正方形,若直线
,短轴端点和焦点所组成的四边形为正方形,若直线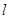 与
与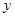 轴交于点
轴交于点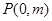 ,与椭圆
,与椭圆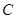 交于不同的两点
交于不同的两点 ,且
,且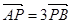 。(14分)
。(14分)
(1)求椭圆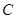 的方程;
的方程;
(2)求实数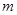 的取值范围。
的取值范围。
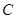 的中心为坐标原点
的中心为坐标原点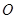 ,一个长轴端点为
,一个长轴端点为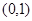 ,短轴端点和焦点所组成的四边形为正方形,若直线
,短轴端点和焦点所组成的四边形为正方形,若直线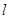 与
与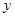 轴交于点
轴交于点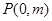 ,与椭圆
,与椭圆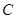 交于不同的两点
交于不同的两点 ,且
,且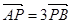 。(14分)
。(14分)(1)求椭圆
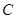 的方程;
的方程;(2)求实数
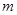 的取值范围。
的取值范围。(1) (2)-1<m<
(2)-1<m< 或
或 <m<1
<m<1
 (2)-1<m<
(2)-1<m< 或
或 <m<1
<m<1试题分析:(1)∵一个长轴端点为
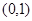 ,所以
,所以 ,且焦点在y轴上,
,且焦点在y轴上,因为短轴端点和焦点所组成的四边形为正方形,所以
 ,
,又因为
 ,所以
,所以 ,所以椭圆方程为
,所以椭圆方程为 .
.(2)(1)当直线
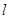 斜率不存在时,不符题意,斜率为0时显然也不符题意;
斜率不存在时,不符题意,斜率为0时显然也不符题意;设
 ,
,由
 ,
,∴
 ,
,设
 ,
,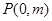 ,
, ,
,所以
 ,
, ,
,所以
 ,所以
,所以 , 消去
, 消去 得
得 ,
,又
 ,∴
,∴ ,
,∴
 , ∴
, ∴ <0, ∴-1<m<
<0, ∴-1<m< 或
或 <m<1.
<m<1.点评:求解直线与圆锥曲线的位置关系时,免不了要联立直线方程和圆锥曲线方程,此时一般运算量比较大,综合考查学生分析问题、解决问题的能力和运算求解能力.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
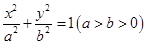 的离心率
的离心率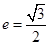 ,且短半轴
,且短半轴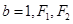 为其左右焦点,
为其左右焦点,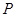 是椭圆上动点.
是椭圆上动点.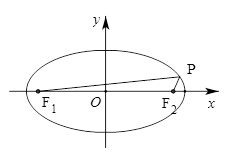
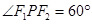 时,求
时,求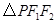 面积;
面积;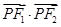 取值范围.
取值范围. 倍
倍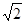 倍
倍 倍
倍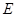 :
: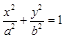 (
(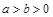 )过点
)过点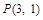 ,其左、右焦点分别为
,其左、右焦点分别为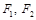 ,且
,且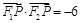 .
.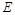 的方程;
的方程;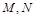 是直线
是直线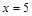 上的两个动点,且
上的两个动点,且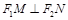 ,则以
,则以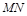 为直径的圆
为直径的圆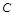 是否过定点?请说明理由.
是否过定点?请说明理由.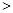 0)的焦点F的直线交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3.则此抛物线的方程为( )
0)的焦点F的直线交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3.则此抛物线的方程为( )
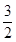 x
x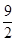 x
x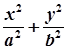 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.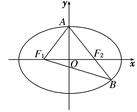
 =2
=2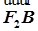 ,
,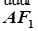 ·
·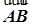 =
=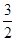 ,求椭圆的方程.
,求椭圆的方程.
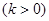 与抛物线
与抛物线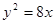 相交于
相交于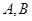 两点,F为抛物线的焦点,若
两点,F为抛物线的焦点,若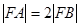 ,则k的值为( )。
,则k的值为( )。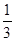
 的两焦点之间的距离为
的两焦点之间的距离为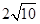
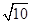
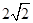
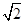
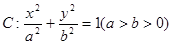 长轴的一个顶点作圆
长轴的一个顶点作圆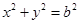 的两条切线,切点分别为
的两条切线,切点分别为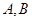 ,若
,若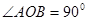 (
(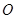 是坐标原点),则椭圆
是坐标原点),则椭圆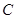 的离心率为_________.
的离心率为_________.