题目内容
对于函数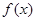 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足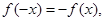 称
称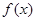 为“局部奇函数”,若
为“局部奇函数”,若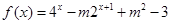 为定义域
为定义域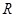 上的“局部奇函数”,则实数的取值范围是( )
上的“局部奇函数”,则实数的取值范围是( )
A.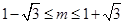 | B. |
C.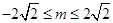 | D.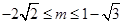 |
B
解析试题分析:当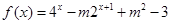 为定义域
为定义域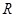 上的“局部奇函数”时,
上的“局部奇函数”时, ,可化为
,可化为 ,令
,令 则
则 ,
, ,从而
,从而 在
在 有解,即可保证
有解,即可保证 为“局部奇函数”,令
为“局部奇函数”,令 ,则 ①当
,则 ①当 时,
时, 在
在 有解,即
有解,即 ,解得
,解得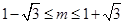 ;②当
;②当 时,
时, 在
在 有解等价于
有解等价于 解得
解得 ;综上可知
;综上可知 ,选B.
,选B.
考点:奇函数的性质、一元二次方程解的分布.

练习册系列答案
相关题目
已知函数f(x)= , 对任意m∈[-3,3],不等式f(mx-1)+f(2x)<0恒成立,则实数x的取值范围为( )
, 对任意m∈[-3,3],不等式f(mx-1)+f(2x)<0恒成立,则实数x的取值范围为( )
A.(-1, ) ) | B.(-2, ) ) | C.(-2, ) ) | D.(-2, ) ) |
下列四个函数中,在区间 上是减函数的是( )
上是减函数的是( )
A. | B. | C. | D. |
函数 的定义域是( )
的定义域是( )
| A.(-1,1) | B. | C. | D.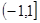 |
已知 ,则
,则 的值是: ( )
的值是: ( )
| A.5 | B.7 | C.8 | D.9 |
设方程 的两个根为
的两个根为 ,则( )
,则( )
A. | B. | C. | D. |
下列函数中与函数f( )=
)= 相同的是( )
相同的是( )
A. | B. | C. | D. |
设P=log23,Q=log32,R=log2(log32),则 ( )
| A.Q<R<P | B.P<R<Q | C.R<Q<P | D.R<P<Q |
已知f(x)=x3-3x+m在区间[0,2]上任取三个数a,b,c,均存在以f(a),f(b),f(c)为边长的三角形,则实数m的取值范围是( )
| A.(6,+∞) | B.(5,+∞) | C.(4,+∞) | D.(3,+∞) |