题目内容
设P=log23,Q=log32,R=log2(log32),则 ( )
| A.Q<R<P | B.P<R<Q | C.R<Q<P | D.R<P<Q |
C.
解析试题分析:题设是三个对数比较大小,因此我们考察相应的对数函数,如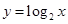 ,
, ,它们都是增函数,从而知
,它们都是增函数,从而知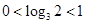 ,
, ,
,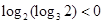 ,因此选C.
,因此选C.
考点:对数函数的单调性.

练习册系列答案
相关题目
已知函数 ,则下列说法不正确的是( )
,则下列说法不正确的是( )
A.当 时,函数 时,函数 有零点 有零点 |
B.若函数 有零点,则 有零点,则 |
C.存在 ,函数 ,函数 有唯一的零点 有唯一的零点 |
D.若函数 有唯一的零点,则 有唯一的零点,则 |
设函数 ,则下列结论错误的是( )
,则下列结论错误的是( )
| A.D(x)的值域为{0,1} | B.D(x)是偶函数 |
| C.D(x)不是周期函数 | D.D(x)不是单调函数 |
下列函数中,既是奇函数又在定义域上单调递增的是( )
A. | B. | C. | D. |
若定义在R上的函数 满足
满足 ,且当
,且当 时,
时, ,函数
,函数 ,则函数
,则函数 在区间
在区间 内的零点个数为( )
内的零点个数为( )
| A.9 | B.7 | C.5 | D.4 |
已知函数 是定义在R上的偶函数, 且在区间
是定义在R上的偶函数, 且在区间 单调递减. 若实数a满足
单调递减. 若实数a满足 , 则a的取值范围是( )
, 则a的取值范围是( )
A.(-∞, ]∪[2,+∞) ]∪[2,+∞) | B. ∪[2,+∞) ∪[2,+∞) |
C. | D. |
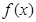 的定义域为
的定义域为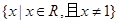 , 且
, 且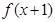 奇函数.当
奇函数.当 时,
时,  -
-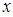 -1,那么函数
-1,那么函数 时,
时, 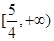
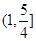
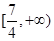
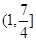
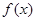 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足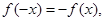 称
称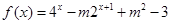 为定义域
为定义域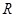 上的“局部奇函数”,则实数的取值范围是( )
上的“局部奇函数”,则实数的取值范围是( )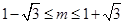

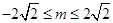
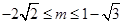
 是定义在实数集R上的奇函数,且当
是定义在实数集R上的奇函数,且当 时,
时, (其中
(其中 是
是 的导函数)恒成立.若
的导函数)恒成立.若 ,
, ,
, ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )


