题目内容
(Ⅰ)设 为正数,且
为正数,且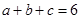 ,求证:
,求证: ;
;
(Ⅱ)设 为正数,
为正数, ,求证:
,求证: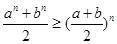
 为正数,且
为正数,且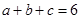 ,求证:
,求证: ;
;(Ⅱ)设
 为正数,
为正数, ,求证:
,求证: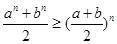
(Ⅰ) 为正数,且
为正数,且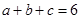 ,由柯西不等式有:
,由柯西不等式有:
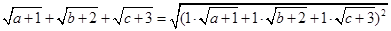
 ,
,
当且仅当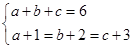 ,即
,即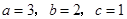 时等号成立,
时等号成立,
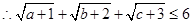 . ……………6分
. ……………6分
(Ⅱ)证法一:用数学归纳法证明:
①当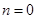 时,左边
时,左边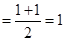 =右边; 当
=右边; 当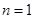 时,左边
时,左边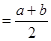 =右边;
=右边;
当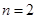 时,左边
时,左边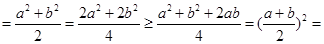 右边,
右边,
所以当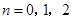 时,不等式
时,不等式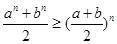 成立;
成立;
②假设当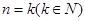 时不等式成立,即
时不等式成立,即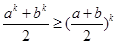 ,则当
,则当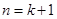 时,
时,
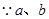 是正数,
是正数,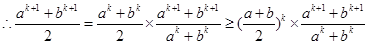 ,
,
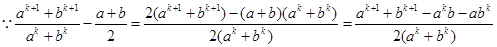
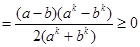 ,
, 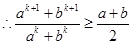 ,
,
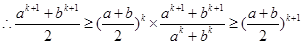
所以当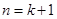 时不等式也成立,
时不等式也成立,
综合①②得当 为正数,
为正数, 时,
时,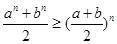 成立. ……………12分
成立. ……………12分
证法二:用构造法证明:
设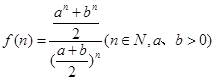 ,则:
,则: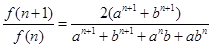 ,
,
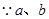 是正数
是正数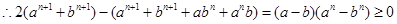 ,
,
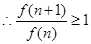 ,又
,又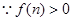 ,
,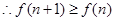 ,
,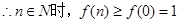 ,
,
即当 为正数,
为正数, 时,
时,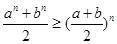 成立.
成立.
 为正数,且
为正数,且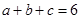 ,由柯西不等式有:
,由柯西不等式有: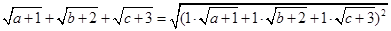
 ,
,当且仅当
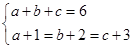 ,即
,即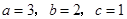 时等号成立,
时等号成立,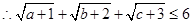 . ……………6分
. ……………6分(Ⅱ)证法一:用数学归纳法证明:
①当
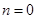 时,左边
时,左边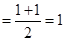 =右边; 当
=右边; 当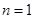 时,左边
时,左边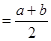 =右边;
=右边;当
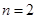 时,左边
时,左边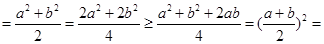 右边,
右边,所以当
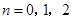 时,不等式
时,不等式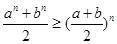 成立;
成立;②假设当
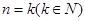 时不等式成立,即
时不等式成立,即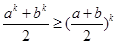 ,则当
,则当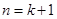 时,
时,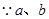 是正数,
是正数,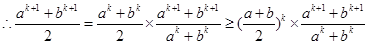 ,
,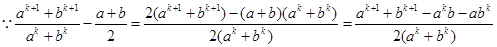
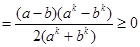 ,
, 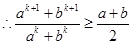 ,
,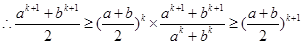
所以当
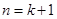 时不等式也成立,
时不等式也成立,综合①②得当
 为正数,
为正数, 时,
时,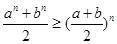 成立. ……………12分
成立. ……………12分证法二:用构造法证明:
设
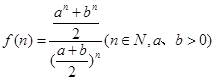 ,则:
,则: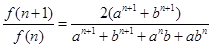 ,
,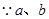 是正数
是正数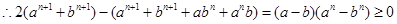 ,
,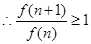 ,又
,又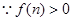 ,
,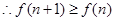 ,
,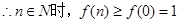 ,
,即当
 为正数,
为正数, 时,
时,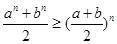 成立.
成立.略

练习册系列答案
相关题目
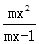 -x>0.
-x>0.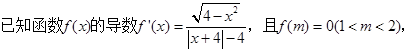 则不等式
则不等式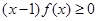 的解集是 .
的解集是 .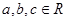 ,且
,且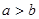 则一定成立的是( )
则一定成立的是( )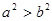
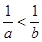
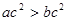
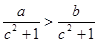
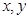 满足
满足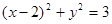 ,则
,则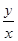 的最大值是____________________;最小值是_________________________;
的最大值是____________________;最小值是_________________________;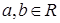 ,则下列命题正确的是( )
,则下列命题正确的是( )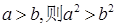
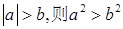
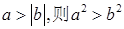
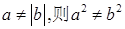
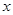 , 若不等式
, 若不等式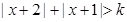 恒成立, 则实数
恒成立, 则实数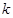 的取值范围是
的取值范围是 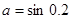 ,
,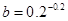 ,
, 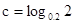 ,则
,则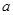 、
、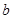 、
、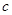 由小到大排列的顺序是____________.
由小到大排列的顺序是____________.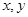 满足
满足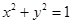 ,则
,则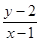 的最小值为 .
的最小值为 .