题目内容
已知集合A={x||x-a|≤1},B={x|x2-4x≥0},若A∩B=?,则实数a的取值范围是
- A.(0,4)
- B.(0,3)
- C.(1,3)
- D.(2,3)
C
分析:先将A,B化简,根据交集的运算,结合数轴,列出关于a的不等式(组),解出即可.
解答:集合A={x||x-a|≤1}={x|-1≤x-a≤1}={x|a-1≤x≤a+1}
B={x|x2-4x≥0}={x|x(x-4)≥0}={x|x≤0或x≥4}
若A∩B=?,则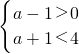
在数轴上表示如下

解得1<a<3.
故选C
点评:本题考查了集合运算中求参数的取值范围,考查了交集运算,空集的概念,数形结合的思想.集合运算若利用数轴这一工具,以形助数,形象直观.则可减少错误,特别是端点值的处理.
本题所列的不等式组中,每一不等式均不能取到等号,否则A∩B≠∅;若将原题集合A,B中等号去掉,则每一不等式反而均应取到等号.读者可通过此题举一反三,把握思路,解决好类似问题.
分析:先将A,B化简,根据交集的运算,结合数轴,列出关于a的不等式(组),解出即可.
解答:集合A={x||x-a|≤1}={x|-1≤x-a≤1}={x|a-1≤x≤a+1}
B={x|x2-4x≥0}={x|x(x-4)≥0}={x|x≤0或x≥4}
若A∩B=?,则
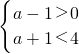
在数轴上表示如下

解得1<a<3.
故选C
点评:本题考查了集合运算中求参数的取值范围,考查了交集运算,空集的概念,数形结合的思想.集合运算若利用数轴这一工具,以形助数,形象直观.则可减少错误,特别是端点值的处理.
本题所列的不等式组中,每一不等式均不能取到等号,否则A∩B≠∅;若将原题集合A,B中等号去掉,则每一不等式反而均应取到等号.读者可通过此题举一反三,把握思路,解决好类似问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目