题目内容
已知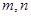 是正整数,
是正整数,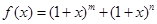 的展开式中
的展开式中 的系数为7.求
的系数为7.求 展开式中
展开式中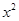 的系数的最小值,并求这时
的系数的最小值,并求这时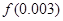 的近似值(精确到0.01).
的近似值(精确到0.01).
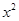 的系数最小值为9,此时
的系数最小值为9,此时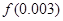 的近似值为
的近似值为 .
.
解析试题分析:先利用二项展开式的通项公式求出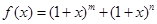 的展开式中的
的展开式中的 的系数
的系数 ,进而由条件得到
,进而由条件得到 ,然后再得到
,然后再得到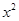 的系数
的系数 ,进而转化成
,进而转化成 ,根据二次函数的图像与性质可确定
,根据二次函数的图像与性质可确定 或
或 时
时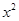 的系数最小,进而根据二项展开式可确定此时
的系数最小,进而根据二项展开式可确定此时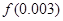 的近似值.
的近似值.
由已知可得 ,则展开式中
,则展开式中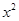 的系数为
的系数为


所以当 或
或 时
时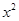 的系数最小为
的系数最小为
这时 ,
,
 .
.
考点:二项式定理.

练习册系列答案
相关题目
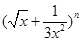 的第五项的二项式系数与第三项的二项式系数的比是
的第五项的二项式系数与第三项的二项式系数的比是 ,
, 的展开式的二项式系数的和比(3x-1)n的展开式的二项式系数和大992,求(2x-
的展开式的二项式系数的和比(3x-1)n的展开式的二项式系数和大992,求(2x-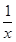 )2n的展开式中,(1)二项式系数最大的项;(2)系数的绝对值最大的项.
)2n的展开式中,(1)二项式系数最大的项;(2)系数的绝对值最大的项.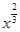 +3x2)n的展开式中,各项系数和比它的二项式系数和大992,求:
+3x2)n的展开式中,各项系数和比它的二项式系数和大992,求: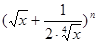 的展开式前三项中的
的展开式前三项中的 的系数成等差数列.
的系数成等差数列. 展开式中不含
展开式中不含 项的系数的和为 .
项的系数的和为 .