题目内容
将抛物线y=x2+4x+7的图象按向量
平移,使其顶点与坐标原点重合,则
=( )
| a |
| a |
| A、(2,-3) |
| B、(-2,-3) |
| C、(-2,3) |
| D、(2,3) |
分析:将抛物y=x2+4x+7的形式加以变化,找出它的顶点,以此点为起点原点为终点,求出向量
的坐标
| a |
解答:解:抛物线y=x2+4x+7可变为(x+2)2=y-3,其顶点坐标是(-2,3)
由题意
=(2,-3)
故选A
由题意
| a |
故选A
点评:本题考查函数的图象与图象的变化,本题考查函数的图象按向量平移,解题的关键是求出原来函数图象顶点的坐标,再根据向量的坐标表示方法求出平移向量的坐标来

练习册系列答案
相关题目
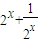 的最小值为2;
的最小值为2;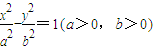 的一条渐近线方程为
的一条渐近线方程为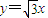 ,且其一个焦点与抛物线y2=8x的焦点重合,则双曲线的离心率为2;
,且其一个焦点与抛物线y2=8x的焦点重合,则双曲线的离心率为2; 个单位,可以得到函数
个单位,可以得到函数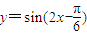 的图象;
的图象;