题目内容
4.已知函数f(x)=f($\frac{1}{x}$),当x∈[1,3]时,f(x)=lnx,在区间[$\frac{1}{3}$,3]内,函数g(x)=f(x)-ax有三个不同的零点,则实数a的取值范围是( )| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{2e}$,$\frac{1}{e}$) | C. | [$\frac{ln3}{3}$,$\frac{1}{e}$) | D. | ($\frac{ln3}{3}$,$\frac{1}{e}$] |
分析 化简可得f(x)=|lnx|,从而作函数f(x)=|lnx|与函数y=ax的图象,从而利用导数及数形结合的思想求解.
解答 解:当x∈[$\frac{1}{3}$,1]时,$\frac{1}{x}$∈[1,3],
故f(x)=f($\frac{1}{x}$)=ln$\frac{1}{x}$=-lnx;
故f(x)=|lnx|,
作函数f(x)=|lnx|与函数y=ax的图象如下,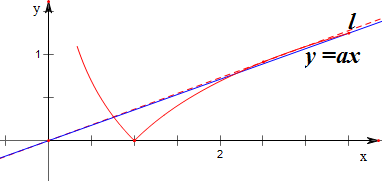 ,
,
设直线l与f(x)=|lnx|相切,如图,设切点为(x,lnx),
则由导数的几何意义可得,$\frac{1}{x}$=$\frac{lnx}{x}$,
故x=e;
故kl=$\frac{1}{e}$;
故实数a的取值范围是[$\frac{ln3}{3}$,$\frac{1}{e}$),
故选:C.
点评 本题考查了导数的几何意义的应用及数形结合的思想应用.

练习册系列答案
相关题目
19.(x-1)11的展开式中含x偶数次幂的项的系数和是( )
| A. | 1024 | B. | -1023 | C. | -1024 | D. | -2048 |
9.函数 y=3-$\frac{3}{1-x}$( )
| A. | 在(-1,+∞)内单调递增 | B. | 在(-1,+∞)内单调递减 | ||
| C. | 在(1,+∞)内单调递增 | D. | 在(1,+∞)内单调递减 |
16.已知函数$f(x)=\left\{\begin{array}{l}x-2,x≥0\\ f(x+2),x<0\end{array}\right.$,则f(-1)=( )
| A. | -1 | B. | 1 | C. | 0 | D. | -3 |
13.命题“?x∈R,f(x)>0”的否定为( )
| A. | ?x0∈R,f(x0)>0 | B. | ?x0∈R,f(x0)≤0 | C. | ?x0∈R,f(x0)≤0 | D. | ?x0∈R,f(x0)>0 |