题目内容
设a为锐角,若cos(a+ )=
)= ,则sin(2a+
,则sin(2a+ )的值为 .
)的值为 .
【答案】分析:根据a为锐角,cos(a+ )=
)= 为正数,可得a+
为正数,可得a+ 也是锐角,利用平方关系可得sin(a+
也是锐角,利用平方关系可得sin(a+ )=
)= .接下来配角,得到cosa=
.接下来配角,得到cosa= ,sina=
,sina= ,再用二倍角公式可得sin2a=
,再用二倍角公式可得sin2a= ,cos2a=
,cos2a= ,最后用两角和的正弦公式得到sin(2a+
,最后用两角和的正弦公式得到sin(2a+ )=sin2acos
)=sin2acos +cosasin
+cosasin =
= .
.
解答:解:∵a为锐角,cos(a+ )=
)= ,
,
∴a+ 也是锐角,且sin(a+
也是锐角,且sin(a+ )=
)= =
=
∴cosa=cos[(a+ )-
)- ]=
]= cos
cos +
+ sin
sin =
=
sina=sin[(a+ )-
)- ]=
]= cos
cos -
- sin
sin =
=
由此可得sin2a=2sinacosa= ,cos2a=cos2a-sin2a=
,cos2a=cos2a-sin2a=
又∵sin =sin(
=sin( )=
)= ,cos
,cos =cos(
=cos( )=
)=
∴sin(2a+ )=sin2acos
)=sin2acos +cosasin
+cosasin =
= •
• +
+ •
• =
=
故答案为:
点评:本题要我们在已知锐角a+ 的余弦值的情况下,求2a+
的余弦值的情况下,求2a+ 的正弦值,着重考查了两角和与差的正弦、余弦公式和二倍角的正弦、余弦等公式,考查了三角函数中的恒等变换应用,属于中档题.
的正弦值,着重考查了两角和与差的正弦、余弦公式和二倍角的正弦、余弦等公式,考查了三角函数中的恒等变换应用,属于中档题.
 )=
)= 为正数,可得a+
为正数,可得a+ 也是锐角,利用平方关系可得sin(a+
也是锐角,利用平方关系可得sin(a+ )=
)= .接下来配角,得到cosa=
.接下来配角,得到cosa= ,sina=
,sina= ,再用二倍角公式可得sin2a=
,再用二倍角公式可得sin2a= ,cos2a=
,cos2a= ,最后用两角和的正弦公式得到sin(2a+
,最后用两角和的正弦公式得到sin(2a+ )=sin2acos
)=sin2acos +cosasin
+cosasin =
= .
.解答:解:∵a为锐角,cos(a+
 )=
)= ,
,∴a+
 也是锐角,且sin(a+
也是锐角,且sin(a+ )=
)= =
=
∴cosa=cos[(a+
 )-
)- ]=
]= cos
cos +
+ sin
sin =
=
sina=sin[(a+
 )-
)- ]=
]= cos
cos -
- sin
sin =
=
由此可得sin2a=2sinacosa=
 ,cos2a=cos2a-sin2a=
,cos2a=cos2a-sin2a=
又∵sin
 =sin(
=sin( )=
)= ,cos
,cos =cos(
=cos( )=
)=
∴sin(2a+
 )=sin2acos
)=sin2acos +cosasin
+cosasin =
= •
• +
+ •
• =
=
故答案为:

点评:本题要我们在已知锐角a+
 的余弦值的情况下,求2a+
的余弦值的情况下,求2a+ 的正弦值,着重考查了两角和与差的正弦、余弦公式和二倍角的正弦、余弦等公式,考查了三角函数中的恒等变换应用,属于中档题.
的正弦值,着重考查了两角和与差的正弦、余弦公式和二倍角的正弦、余弦等公式,考查了三角函数中的恒等变换应用,属于中档题. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
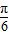 )=
)= ,则sin(2a+
,则sin(2a+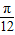 )的值为 .
)的值为 .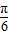 )=
)= ,则sin(2a+
,则sin(2a+ )的值为 .
)的值为 . )=
)= ,则sin(2a+
,则sin(2a+ )的值为 .
)的值为 . )=
)= ,则sin(2a+
,则sin(2a+ )的值为 .
)的值为 .