题目内容
如图,在正方体ABCD-A1B1C1D1中,M、N分别是棱CD、CC1的中点,则异面直线A1M与DN所成的角的大小是( )
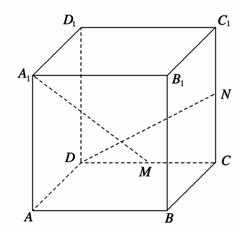
A.30° B.45°
C.60° D.90°
D
[解析] 解法1:取CN的中点H,连接MH、A1H,则MH=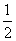 DN.
DN.

设正方体的棱长为2,则DN= ,MH=
,MH= ,
,
A1M2=22+22+12=9.
从而A1H2=(2-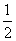 )2+22+22=
)2+22+22=
∵A1H2=MH2+A1M2,∴∠A1MH=90°
解法2:以D为原点,DA、DC、DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,设AB=1,则D(0,0,0),N(0,1,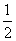 ),M(0,
),M(0,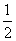 ,0),A1(1,0,1),∴
,0),A1(1,0,1),∴ =(0,1,
=(0,1,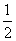 ),
), =(1,-
=(1,-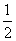 ,1),∴
,1),∴ ·
· =0,∴
=0,∴ ⊥
⊥ ,
,
∴A1M与DN所成角的大小为90°.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
 取得最小值时的点P的坐标是______.
取得最小值时的点P的坐标是______.
 D.以上都不对
D.以上都不对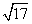 ,则该二面角的大小为( )
,则该二面角的大小为( )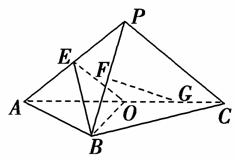
 B.-
B.-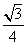
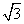 ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.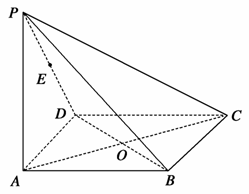
 的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=40°,过点A作截面AEF,则截面△AEF周长的最小值为________.
的正三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=40°,过点A作截面AEF,则截面△AEF周长的最小值为________.