题目内容
设正实数x,y,z满足x2-3xy+4y2-z=0.则当
取得最大值时,
+
-
的最大值为( )
| xy |
| z |
| 2 |
| x |
| 1 |
| y |
| 2 |
| z |
| A.0 | B.1 | C.
| D.3 |
∵x2-3xy+4y2-z=0,
∴z=x2-3xy+4y2,又x,y,z均为正实数,
∴
=
=
≤
=1(当且仅当x=2y时取“=”),
∴(
)max=1,此时,x=2y.
∴z=x2-3xy+4y2=(2y)2-3×2y×y+4y2=2y2,
∴
+
-
=
+
-
=-(
-1)2+1≤1.
∴
+
-
的最大值为1.
故选B.
∴z=x2-3xy+4y2,又x,y,z均为正实数,
∴
| xy |
| z |
| xy |
| x2-3xy+4y2 |
| 1 | ||||
|
| 1 | ||||||
2
|
∴(
| xy |
| z |
∴z=x2-3xy+4y2=(2y)2-3×2y×y+4y2=2y2,
∴
| 2 |
| x |
| 1 |
| y |
| 2 |
| z |
| 1 |
| y |
| 1 |
| y |
| 1 |
| y2 |
| 1 |
| y |
∴
| 2 |
| x |
| 1 |
| y |
| 2 |
| z |
故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的最小值为________.
的最小值为________. 的最小值为 .
的最小值为 .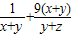 的最小值为 .
的最小值为 . 的最小值为 .
的最小值为 .