题目内容
函数f（x）=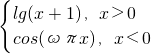
图象上关于坐标原点O对称的点恰有5对，则ω的值可以为
- A.
- B.
- C.
- D.
B
分析：要求函数图象上关于坐标原点对称，则有f（-x）=-f（x），转化为方程根的个数，再用数形结合法求解．
解答：
解：当x＜0时，-x＞0
若函数f（x）=图象上关于坐标原点O对称
则有-lg（x+1）=cosωπx，
令：y=-lg（-x+1），y=cosωπx，
图象上关于坐标原点O对称的点有5对，则y=-lg（-x+1）与y=cosωπx（x＜0）的图象有5个交点
∴-
=-9
∴ω=
故选B
点评：本题主要通过分段函数来考查函数奇偶性的应用，同时还考查了学生作图和数形结合的能力．
分析：要求函数图象上关于坐标原点对称，则有f（-x）=-f（x），转化为方程根的个数，再用数形结合法求解．
解答：
解：当x＜0时，-x＞0若函数f（x）=图象上关于坐标原点O对称
则有-lg（x+1）=cosωπx，
令：y=-lg（-x+1），y=cosωπx，
图象上关于坐标原点O对称的点有5对，则y=-lg（-x+1）与y=cosωπx（x＜0）的图象有5个交点
∴-
=-9∴ω=
故选B
点评：本题主要通过分段函数来考查函数奇偶性的应用，同时还考查了学生作图和数形结合的能力．
练习册系列答案
快乐5加2金卷系列答案
相关题目