题目内容
若
，则α∈
- A.
- B.
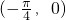
- C.
- D.
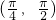
B
分析：先根据sinα＞
，整理求得sinα＜0，判断出α的范围，进而根据tanα＞cota转化成正弦和余弦，可推断＞-1，进而根据正切函数的单调性求得α的范围，最后综合答案可得．
解答：∵sinα＞，
∴cosαsinα-sinα＞0，即sinα（cosα-1）＞0
∵cosα-1＜0
∴sinα＜0，-
＜α＜0
∵tanα＞cota
∴＞
∵-＜α＜0
∴＞-1
即tanα＞-1
∴α＞-
综合得-＜α＜0
故选B
点评：本题主要考查了弦切互化的问题．解题的关键是通过弦切的互化找的解决问题的突破口．
分析：先根据sinα＞
，整理求得sinα＜0，判断出α的范围，进而根据tanα＞cota转化成正弦和余弦，可推断＞-1，进而根据正切函数的单调性求得α的范围，最后综合答案可得．解答：∵sinα＞
，∴cosαsinα-sinα＞0，即sinα（cosα-1）＞0
∵cosα-1＜0
∴sinα＜0，-
＜α＜0∵tanα＞cota
∴
＞∵-
＜α＜0∴
＞-1即tanα＞-1
∴α＞-
综合得-
＜α＜0故选B
点评：本题主要考查了弦切互化的问题．解题的关键是通过弦切的互化找的解决问题的突破口．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
与抛物线
相交于
两点，
为
的焦点，若
，则
( )
B.
C. 
D. 
中，内角
的对边分别是
若
，则
=( )
B.
C.
D.
，则a,b,c的大小关系是 ．
，
，若
，则
(
)
B.
C.0 D.1
，则
(B)
(C)
(D)