��Ŀ����
��ԲC1��
+
=1��a��b��0���ij��᳤Ϊ4������Ϊ2��F1��F2�ֱ�Ϊ��Բ�����ҽ��㣬ֱ��l1����F1�Ҵ�ֱ����Բ�ij��ᣬ��ֱ��l2��ֱl1�ڵ�P���߶�PF2��ֱƽ���߽�l2�ڵ�M
��1������ԲC1�ı����̺Ͷ���M�Ĺ켣C2�ķ��̣�
��2������ԲC1���ҽ���F2��б��Ϊ1��ֱ�߽���Բ��A��B���㣬���ABF1�������
��3����켣C2��x�ύ�ڵ�Q����ͬ������R��S�ڹ켣C2�ϣ�
����
•
=0��֤��ֱ��RS���x���ϵĶ��㣮
| x2 |
| a2 |
| y2 |
| b2 |
��1������ԲC1�ı����̺Ͷ���M�Ĺ켣C2�ķ��̣�
��2������ԲC1���ҽ���F2��б��Ϊ1��ֱ�߽���Բ��A��B���㣬���ABF1�������
��3����켣C2��x�ύ�ڵ�Q����ͬ������R��S�ڹ켣C2�ϣ�
����
| QR |
| QS |
��������1��������֪��2a=4����a=2��2c=2����c=1��b2=a2-c2=3������Բ����Ϊ
+
=1����MP=MF2��֪����M����ֱ��l1��x=-1���ľ��������������F1��1��0���ľ��룬�ɴ��������M�Ĺ켣C2�ķ��̣�
��2��
��ȥx�������ã�7y2+6y-9=0����A��x3��y3����B��x4��y4����y3+y4=-
��y3y4=-
���ɴ��������ABF1�������
��3��Q��0��0������R(
��y1) ��S(
��y2)��kRS=
=
����
•
=0��֪
+y1y2=0��������ֱ֪��RS������㣨4��0����
| x2 |
| 4 |
| y2 |
| 3 |
��2��
|
| 6 |
| 7 |
| 9 |
| 7 |
��3��Q��0��0������R(
| y12 |
| 4 |
| y22 |
| 4 |
| y2-y1 | ||||
|
| 4 |
| y1+y2 |
| QR |
| QS |
| ||||
| 16 |
����⣺��1��������֪��2a=4����a=2��2c=2����c=1��b2=a2-c2=3������Բ����Ϊ
+
=1����MP=MF2��֪
�ද��M����ֱ��l1��x=-1���ľ��������������F1��1��0���ľ��룬
�ද��M�Ĺ켣��CΪl1�ߣ�F2Ϊ�����������
���M�Ĺ켣C2�ķ���Ϊy2=4x��5�֣�
��2��
��ȥx�������ã�7y2+6y-9=0
��A��x3��y3����B��x4��y4����y3+y4=-
��y3y4=-
��7�֣�S��ABF1=
|F1F2|•|y3-y4|=|y3-y4|=
=
��9�֣�
��3��Q��0��0������R(
��y1) ��S(
��y2)��kRS=
=
��10�֣���
•
=0��
+y1y2=0��y1��0��y2��0��y1y2=-16x1x2=16��11�֣���ֱ��RS��y-y1=
(x-x1)��y=
x+y1-
��y=
x+
=
x+
=
x+
=
x+
=
(x-4)��13�֣�
��ֱ��RS������㣨4��0����14�֣�
| x2 |
| 4 |
| y2 |
| 3 |
�ද��M����ֱ��l1��x=-1���ľ��������������F1��1��0���ľ��룬
�ද��M�Ĺ켣��CΪl1�ߣ�F2Ϊ�����������
���M�Ĺ켣C2�ķ���Ϊy2=4x��5�֣�
��2��
|
��A��x3��y3����B��x4��y4����y3+y4=-
| 6 |
| 7 |
| 9 |
| 7 |
| 1 |
| 2 |
| (y3+y4)2-4y3y4 |
12
| ||
| 7 |
��3��Q��0��0������R(
| y12 |
| 4 |
| y22 |
| 4 |
| y2-y1 | ||||
|
| 4 |
| y1+y2 |
| QR |
| QS |
| ||||
| 16 |
| 4 |
| y1+y2 |
| 4 |
| y1+y2 |
| 4x1 |
| y1+y2 |
| 4 |
| y1+y2 |
| y1(y1+y2)-4x1 |
| y1+y2 |
| 4 |
| y1+y2 |
| ||||||
| y1+y2 |
| 4 |
| y1+y2 |
| y1y2 |
| y1+y2 |
| 4 |
| y1+y2 |
| -16 |
| y1+y2 |
| 4 |
| y1+y2 |
��ֱ��RS������㣨4��0����14�֣�
���������⿼��ֱ�ߺ�Բ���ߵ�λ�ù�ϵ������ʱҪ�������⣬ע������ؽ��еȼ�ת����

��ϰ��ϵ�д�
�����Ŀ
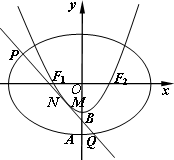 ����ԲC1��
����ԲC1��