题目内容
((本小题满分12分)
已知椭圆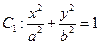 的左、右两个焦点为
的左、右两个焦点为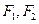 ,离心率为
,离心率为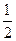 ,又抛物线
,又抛物线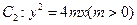 与椭圆
与椭圆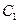 有公共焦点
有公共焦点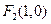 .
.
(1)求椭圆和抛物线的方程;
(2)设直线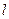 经过椭圆的左焦点
经过椭圆的左焦点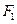 且与抛物线交于不同两点P、Q且满足
且与抛物线交于不同两点P、Q且满足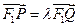 ,求实数
,求实数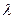 的取值范围.
的取值范围.
已知椭圆
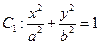 的左、右两个焦点为
的左、右两个焦点为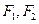 ,离心率为
,离心率为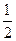 ,又抛物线
,又抛物线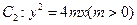 与椭圆
与椭圆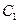 有公共焦点
有公共焦点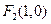 .
.(1)求椭圆和抛物线的方程;
(2)设直线
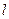 经过椭圆的左焦点
经过椭圆的左焦点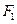 且与抛物线交于不同两点P、Q且满足
且与抛物线交于不同两点P、Q且满足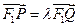 ,求实数
,求实数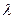 的取值范围.
的取值范围.(1)椭圆中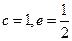 ,所以
,所以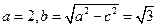 ,椭圆方程为:
,椭圆方程为: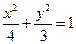
抛物线中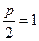 ,所以
,所以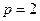 ,抛物线方程为:
,抛物线方程为: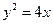 4分
4分
(2)设直线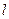 的方程为:
的方程为: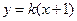 ,和抛物线方程联立得
,和抛物线方程联立得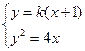
消去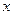 ,整理得
,整理得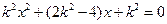
因为直线和抛物线有两个交点,所以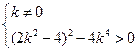
解得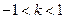 且
且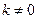 7分
7分
设 ,则
,则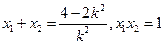
又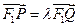 ,所以
,所以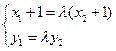
又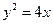 ,由此得
,由此得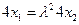 ,即
,即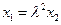 9分
9分
由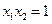 ,解得
,解得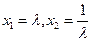
又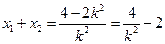 ,所以,
,所以,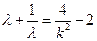 11分
11分
又因为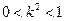 ,所以
,所以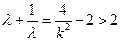 ,解得
,解得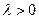 且
且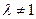 13分
13分
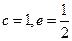 ,所以
,所以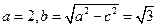 ,椭圆方程为:
,椭圆方程为: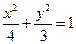
抛物线中
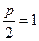 ,所以
,所以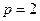 ,抛物线方程为:
,抛物线方程为: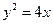 4分
4分(2)设直线
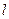 的方程为:
的方程为: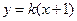 ,和抛物线方程联立得
,和抛物线方程联立得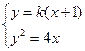
消去
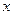 ,整理得
,整理得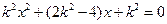
因为直线和抛物线有两个交点,所以
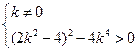
解得
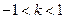 且
且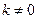 7分
7分设
 ,则
,则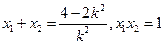
又
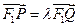 ,所以
,所以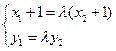
又
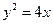 ,由此得
,由此得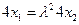 ,即
,即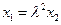 9分
9分由
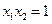 ,解得
,解得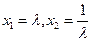
又
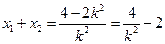 ,所以,
,所以,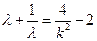 11分
11分又因为
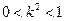 ,所以
,所以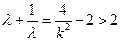 ,解得
,解得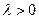 且
且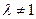 13分
13分略

练习册系列答案
相关题目
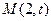
 在直线
在直线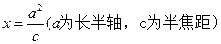 上。
上。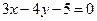 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;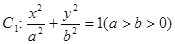 的左准线为
的左准线为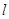 ,左右焦点分别为
,左右焦点分别为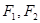 ,抛物线
,抛物线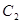 的准线为
的准线为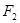 ,曲线
,曲线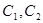 的一个交点为P,则
的一个交点为P,则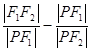 等于()
等于()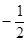 D
D 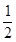
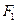 (-3,0
(-3,0 )
)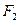 (3,0),P为椭圆上一点,且
(3,0),P为椭圆上一点,且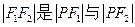 的等差中项,则椭圆的方程为___________________________.
的等差中项,则椭圆的方程为___________________________.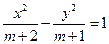 表示椭圆,则实数
表示椭圆,则实数 的取值范围是____________________;
的取值范围是____________________;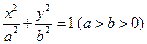 的
的 左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴, 直线AB交
左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴, 直线AB交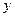 轴于点P,若
轴于点P,若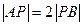 ,则椭圆的离心率是( )
,则椭圆的离心率是( )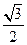

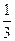
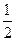
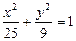 的焦点F1 、F2,P为椭圆上的一点,已知
的焦点F1 、F2,P为椭圆上的一点,已知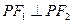 ,则
,则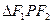
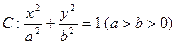 ,过右焦点
,过右焦点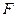 斜率为
斜率为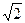 的直线与椭圆
的直线与椭圆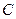 交于
交于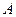 、
、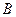 两
两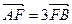 ,则椭圆
,则椭圆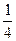

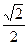
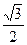
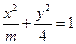 的焦距为2,则m的值等于
的焦距为2,则m的值等于