题目内容
定义在区间[0,1]上的函数f(x),f(0)=f(1)=0,且对任意的x1,x2∈[0,1],都有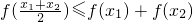 ,则
,则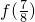 =________.
=________.
0
分析:先令x1=x2=x,推出对任意x∈[0,1],f(x)≥0,再由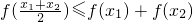 ,分别推出f(
,分别推出f( )≤0,f(
)≤0,f( )≤0,f(
)≤0,f( )≤0,从而f(
)≤0,从而f( )=0,f(
)=0,f( )=0,f(
)=0,f( )=0
)=0
解答:令x1=x2=x∈[0,1],则f(x)≤2f(x),即f(x)≥0
∵f( )=f(
)=f(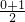 )≤0
)≤0
∴f( )=0
)=0
∵f( )=f(
)=f(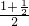 )≤0
)≤0
∴f( )=0
)=0
∵f( )=f(
)=f( )≤0
)≤0
∴f( )=0
)=0
故答案为 0
点评:本题考查了抽象函数表达式的运用,解题时要善于观察,善于利用抽象表达式推出函数性质和特殊函数值
分析:先令x1=x2=x,推出对任意x∈[0,1],f(x)≥0,再由
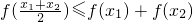 ,分别推出f(
,分别推出f( )≤0,f(
)≤0,f( )≤0,f(
)≤0,f( )≤0,从而f(
)≤0,从而f( )=0,f(
)=0,f( )=0,f(
)=0,f( )=0
)=0解答:令x1=x2=x∈[0,1],则f(x)≤2f(x),即f(x)≥0
∵f(
 )=f(
)=f(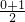 )≤0
)≤0∴f(
 )=0
)=0∵f(
 )=f(
)=f(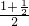 )≤0
)≤0∴f(
 )=0
)=0∵f(
 )=f(
)=f( )≤0
)≤0∴f(
 )=0
)=0故答案为 0
点评:本题考查了抽象函数表达式的运用,解题时要善于观察,善于利用抽象表达式推出函数性质和特殊函数值

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,下列结论正确的是( )
| A、f(x2)-f(x1)>x2-x1 | ||||
| B、f(x2)-f(x1)<x2-x1 | ||||
C、
| ||||
| D、x2f(x1)>x1f(x2) |
 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论:
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1、x2,给出下列结论: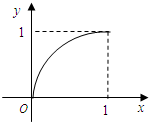 已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论:
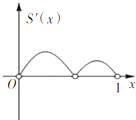
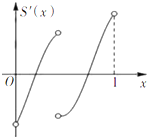
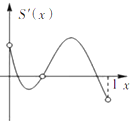
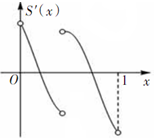
已知定义在区间[0,1]上的函数y=f(x)的图象如图所示,对于满足0<x1<x2<1的任意x1,x2,给出下列结论: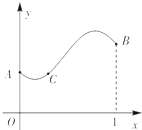 定义在区间[0,1]上的函数f(x)的图象如图所示,以A(0,f(0))、B(1,f(1))、C(x,f(x))为顶点的△ABC的面积记为函数S(x),则函数S(x)的导函数S′(x)的大致图象为( )
定义在区间[0,1]上的函数f(x)的图象如图所示,以A(0,f(0))、B(1,f(1))、C(x,f(x))为顶点的△ABC的面积记为函数S(x),则函数S(x)的导函数S′(x)的大致图象为( )