题目内容
在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,S D=![]() ,在线段SA上取一点E(不含端点)使EC=AC,截面CDE与SB交于点F。
,在线段SA上取一点E(不含端点)使EC=AC,截面CDE与SB交于点F。
(1)求证:四边形EFCD为直角梯形;
(2)设SB的中点为M,当![]() 的值是多少时,能使△DMC
的值是多少时,能使△DMC
为直角三角形?![]() 请给出证明.
请给出证明.
解:(1)∵ CD∥AB,AB![]() 平面SAB ∴CD∥平面SAB
平面SAB ∴CD∥平面SAB
面EFCD∩面SAB=EF,
 ∴CD∥EF ∵
∴CD∥EF ∵![]()
又![]() 面
面![]()
∴![]()
![]() 平面SAD,∴
平面SAD,∴![]() 又
又![]()
![]() 为直角梯形
为直角梯形
(2)当![]() 时,
时,![]() 为直角三角形 .
为直角三角形 .
![]()
![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
在![]() 中,
中,![]() 为SB中点,
为SB中点,![]() .
.
![]() 平面
平面![]()
![]() 平面
平面![]()
![]() 为直角三角形。
为直角三角形。

练习册系列答案
相关题目
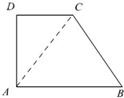
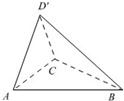
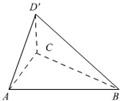
 (2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
(2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
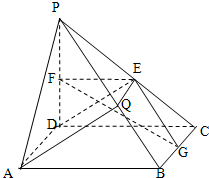
 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD= 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为