题目内容
已知锐角α,β满足cosα=
解:∵α为锐角,且cosα=![]() ,
,
∴sinα=![]() .又∵0<α<
.又∵0<α<![]() ,0<β<
,0<β<![]() ,∴-
,∴-![]() <α-β<
<α-β<![]() .
.
又∵tan(α-β)=-![]() <0,
<0,
∴cos(α-β)=![]() .
.
从而sin(α-β)=tan(α-β)cos(α-β)=-![]() .
.
∴cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)
=![]() .
.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目







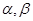 满足:
满足: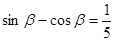 ,
, ,则
,则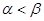 B.
B.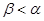 C.
C.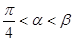 D.
D.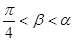
 满足
满足 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 满足
满足 ,
, ,则
,则 等于
等于 B.
B.
 C.
C.
 D.
D.
