题目内容
已知函数
的图象过
，且
内角A、B、C所对应边分别为a、b、c，若
①求
的值及
的单调递增区间
②求的面积。
【答案】
⑴
的单调递减增区间为
⑵
的面积为
或
【解析】（1）由
，求出
的值，再利用三角函数的公式把
化简为
的形式，根据正弦函数的单调性求得增区间；（2）由
和
的范围，求出，再根据正弦定理和面积公式可解答。
⑴ 
（2分）
的单调递减增区间为 （7分）
⑵
正弦定理得 
或
当
时，得
则 
当时，得
则 
的面积为或
练习册系列答案
相关题目
的图象过点（—1，—6），且函数
的图象关于y轴对称。 （1）求m、n的值及函数y=f(x)的单调区间；（2）若a＞0，求函数y=f(x)在区间（a-1,a+1）内的极值. w.w.w.k.s.5.u.c.o.m 
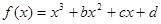的图象过点P
,
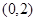且在点M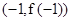
处的切线方程为
.
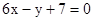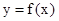的解析式; (2) 求函数
的图象过点
，且它在
处的切线方程为
.
，不等式
恒成立，则实数
的取值范围__________..
的图象过
，且△ABC内角A．B．C所对应边分别为a．b．c，若