Question

设函数f(x)=ax³+bx²+cx,在x=1和x=-1处有极值，且f(1)=-1,求a、b、c并求其极值.

Answer 1

思路分析：此题属于逆向思维，仍可根据求函数极值的步骤来求，但要注意极值点与导数之间的关系：极值点为f′(x)=0的根.利用这一关系，来用待定系数法求a、b、c.

解:f′(x)=3ax²+2bx+c

∵x=1,x=-1为函数极值点

则1,-1为方程f′(x)=0即3ax²+2bx+c=0的两根

∴

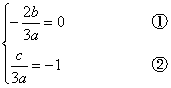
又f(1)=-1,

∴a+b+c=-1                         ③

解得a=,b=0,c=-,此时f(x)=x³-x,f′(x)= x²-

列表：

x	(-∞,-1)	-1	(-1,1)	1	(1,+∞)
y′	+	0	-	0	+
y		极大值1		极小值-1

∴y_极大=y|_x=-1=1,y_极小=y|_x=1=-1