题目内容
如果某日在亚丁湾担任护航任务的我海军“马鞍山”舰向西以4
海里/小时的速度朝灯塔Q方向,当行驶至距离灯塔3
三海里的A处,通过卫星导航系统发现有一可疑小艇位于灯塔的北偏东60°的方向,距灯塔1海里B处,正以4海里/小时的速度朝北偏东60°方向行驶.
(1)t小时后,小艇与“马鞍山”舰相距多少海里?
(2)什么时候两船距离最近?
| 3 |
| 3 |
(1)t小时后,小艇与“马鞍山”舰相距多少海里?
(2)什么时候两船距离最近?
考点:解三角形的实际应用
专题:解三角形
分析:(1)如图所示,由题意可得:当t∈[0,
]小时,小艇距灯塔Q有1+4t海里,“马鞍山”舰距灯塔Q,3
-4
t海里;利用余弦定理可得CD=
海里.
当t∈(
,+∞)小时,利用余弦定理可得相距CD=
海里.
(2)利用二次函数的单调性即可得出.
| 3 |
| 4 |
| 3 |
| 3 |
| 112t2-88t+19 |
当t∈(
| 3 |
| 4 |
| 16t2-40t+37 |
(2)利用二次函数的单调性即可得出.
解答:
解:(1)如图所示,
由题意可得:当t∈[0,
]小时,小艇距灯塔Q有1+4t海里,“马鞍山”舰距灯塔Q,3
-4
t海里;
此时小艇与“马鞍山”舰相距CD=
=
海里.
当t∈(
,+∞)小时,小艇距灯塔Q有1+4t海里,“马鞍山”舰距灯塔Q,4
t-3
海里.
此时小艇与“马鞍山”舰相距=
=
海里.
(2)由(1)可得:当t∈[0,
]小时,小艇与“马鞍山”舰相距CD=
.
当t=
时,CD取得最小值
.
当t∈(
,+∞)小时后,此时小艇与“马鞍山”舰相距CD=
海里.
当t=
时,CD取得最小值2
.
而
<2
.
∴当t=
时,CD取得最小值
.

由题意可得:当t∈[0,
| 3 |
| 4 |
| 3 |
| 3 |
此时小艇与“马鞍山”舰相距CD=
(1+4t)2+(3
|
| 112t2-88t+19 |
当t∈(
| 3 |
| 4 |
| 3 |
| 3 |
此时小艇与“马鞍山”舰相距=
(1+4t)2+(4
|
| 16t2-40t+37 |
(2)由(1)可得:当t∈[0,
| 3 |
| 4 |
| 112t2-88t+19 |
当t=
| 11 |
| 28 |
2
| ||
| 7 |
当t∈(
| 3 |
| 4 |
| 16t2-40t+37 |
当t=
| 5 |
| 4 |
| 3 |
而
2
| ||
| 7 |
| 3 |
∴当t=
| 11 |
| 28 |
2
| ||
| 7 |
点评:本题考查了余弦定理的应用、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若实数x,y满足不等式
,且目标函数z=x-2y的最大值为( )
|
| A、1 | B、2 | C、3 | D、4 |
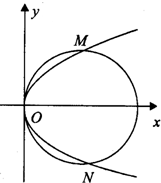 如图,曲线c1:y2=2px(p>0)与曲线c2:(x-6)2+y2=36只有三个公共点O,M,N,其中O为坐标原点,且
如图,曲线c1:y2=2px(p>0)与曲线c2:(x-6)2+y2=36只有三个公共点O,M,N,其中O为坐标原点,且