Question

若函数f(x)＝ax³－bx＋4，当x＝2时，函数f(x)有极值－.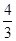

(1)求函数的解析式．

(2)若方程f(x)＝k有3个不同的根，求实数k的取值范围．

 

Answer 1

【答案】

(1) f(x)＝x³－4x＋4.(2)－<k<.

【解析】

试题分析：f′(x)＝3ax²－b.

(1)由题意得解得

故所求函数的解析式为f(x)＝x³－4x＋4.

(2)由(1)可得f′(x)＝x²－4＝(x－2)(x＋2)，

令f′(x)＝0，得x＝2或x＝－2.

当x变化时，f′(x)，f(x)的变化情况如下表：

x	(－∞，－2)	－2	(－2，2)	2	(2，＋∞)
f′(x)	＋	0	－	0	＋
f(x)	?		?	－

因此，当x＝－2时，f(x)有极大值，

当x＝2时，f(x)有极小值－，

所以函数f(x)＝x³－4x＋4的图象大致如图所示．

若f(x)＝k有3个不同的根，则直线y＝k与函数f(x)的图象有3个交点，所以－<k<.

考点：本题主要考查函数的解析式，应用导数研究函数的单调性、极值。

点评：中档题，利用导数研究函数的单调性、极值、最值，是导数的应用中的基本问题。本题（II）应用导数，通过研究函数的单调性、极值等，对函数的图象有了充分的了解，明确了函数零点情况。