题目内容
已知集合A={x|（x-2）[x-（3a+1）]＜0}，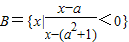
．（Ⅰ）当a=2时，求A∩B；
（Ⅱ）求使B⊆A的实数a的取值范围．
【答案】分析：（Ⅰ）当a=2时，先化简集合A和B，后再求交集即可；
（Ⅱ）先化简集合B：B={x|a＜x＜a2+1}，再根据题中条件：“B⊆A”对参数a分类讨论：①当3a+1=2，②当3a+1＞2，③当3a+1＜2，分别求出a的范围，最后进行综合即得a的范围．
解答：解：（Ⅰ）当a=2时，A={x|2＜x＜7}，B={x|2＜x＜5}
∴A∩B={x|2＜x＜5}（4分）
（Ⅱ）∵（a2+1）-a=（a-
）2+
＞0，即a2+1＞a
∴B={x|a＜x＜a2+1}
①当3a+1=2，即a=
时A=Φ，不存在a使B⊆A（6分）
②当3a+1＞2，即a＞
时A={x|2＜x＜3a+1}由B⊆A得：
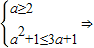2≤a≤3（8分）
③当3a+1＜2，即a＜
时A={x|3a+1＜x＜2}由B⊆A得
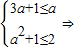-1≤a≤-
?（12分）
综上，a的范围为：[-1，-
]∪[2，3]（14分）
点评：本小题主要考查集合的包含关系判断及应用、交集及其运算、不等式的解法等基础知识，考查运算求解能力，考查分类讨论思想．属于基础题．
（Ⅱ）先化简集合B：B={x|a＜x＜a2+1}，再根据题中条件：“B⊆A”对参数a分类讨论：①当3a+1=2，②当3a+1＞2，③当3a+1＜2，分别求出a的范围，最后进行综合即得a的范围．
解答：解：（Ⅰ）当a=2时，A={x|2＜x＜7}，B={x|2＜x＜5}
∴A∩B={x|2＜x＜5}（4分）
（Ⅱ）∵（a2+1）-a=（a-
）2+＞0，即a2+1＞a∴B={x|a＜x＜a2+1}
①当3a+1=2，即a=
时A=Φ，不存在a使B⊆A（6分）②当3a+1＞2，即a＞
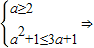时A={x|2＜x＜3a+1}由B⊆A得：2≤a≤3（8分）③当3a+1＜2，即a＜
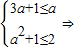时A={x|3a+1＜x＜2}由B⊆A得-1≤a≤-?（12分）综上，a的范围为：[-1，-
]∪[2，3]（14分）点评：本小题主要考查集合的包含关系判断及应用、交集及其运算、不等式的解法等基础知识，考查运算求解能力，考查分类讨论思想．属于基础题．
练习册系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目