题目内容
已知函数 ,
, .
.
(1)若 ,求证:当
,求证:当 时,
时, ;
;
(2)若 在区间
在区间 上单调递增,试求
上单调递增,试求 的取值范围;
的取值范围;
(3)求证: .
.
(1)详见解析;(2)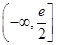 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)将 代入函数解析式,利用导数函数
代入函数解析式,利用导数函数 在区间
在区间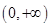 上的单调性,进而由单调性证明
上的单调性,进而由单调性证明 ;(2)解法一是“将函数
;(2)解法一是“将函数 在区间
在区间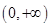 上单调递增”转化为“不等式
上单调递增”转化为“不等式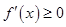 在区间
在区间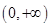 上恒成立”,然后利用参数分离法等价转化为“不等式
上恒成立”,然后利用参数分离法等价转化为“不等式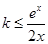 在区间
在区间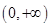 上恒成立”,最终转化为
上恒成立”,最终转化为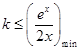 ;解法二是先将问题转化为
;解法二是先将问题转化为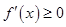 在区间
在区间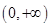 上恒成立,对参数
上恒成立,对参数 进行分类讨论,围绕
进行分类讨论,围绕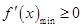 ,从而对参数
,从而对参数 进行求解;(3)先将不等式等价转化证明
进行求解;(3)先将不等式等价转化证明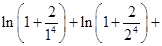
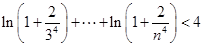 ,在(2)中,令
,在(2)中,令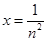 得到
得到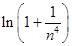 ,然后在(2)中得到
,然后在(2)中得到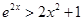 ,两边取对数得到
,两边取对数得到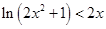 ,在令
,在令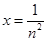 ,得到
,得到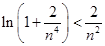 ,再结合放缩法得到
,再结合放缩法得到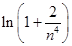
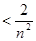
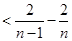 ,需注意第一个不等式不用放缩法,即
,需注意第一个不等式不用放缩法,即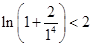 ,利用累加法便可得到
,利用累加法便可得到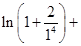
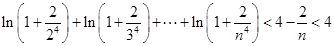 ,从而证明相应的不等式.
,从而证明相应的不等式.
试题解析:(1)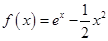 ,则
,则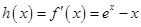 ,
,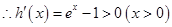 ,
, 在
在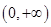 上单调递增,
上单调递增,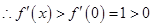 ,
,
故函数 在
在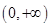 上单调递增,所以
上单调递增,所以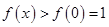 ;
;
(2)解法一: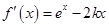 ,下求使
,下求使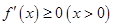 恒成立的
恒成立的 的取值范围.
的取值范围.
当 时,由
时,由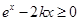 ,得
,得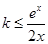 在
在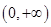 上恒成立,
上恒成立,
令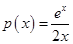 ,则有
,则有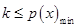 ,则
,则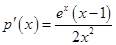 ,令
,令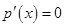 ,解得
,解得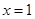 ,
,
列表如下: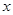
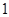
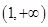
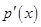
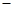

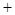
 练习册系列答案
练习册系列答案

西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
相关题目
 .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 的单调性.
的单调性. 为
为 的
的 阶函数.
阶函数. 的单调区间;
的单调区间; 的解的个数;
的解的个数; .
.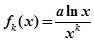 为
为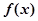 的
的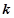 阶函数.
阶函数.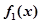 的单调区间;
的单调区间;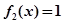 的解的个数;
的解的个数; .
. 的图象在
的图象在 上连续,定义:
上连续,定义: ,
,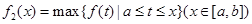 .其中,
.其中, 表示函数
表示函数 上的最小值,
上的最小值, 表示函数
表示函数 ,使得
,使得 对任意的
对任意的 成立,则称函数
成立,则称函数 ,试写出
,试写出 ,
, 的表达式;
的表达式; ,试判断
,试判断 上的“
上的“ ,函数
,函数 是
是 上的2阶收缩函数,求
上的2阶收缩函数,求 的取值范围.
的取值范围.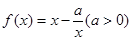 ,
,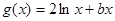 ,且直线
,且直线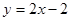 与曲线
与曲线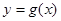 相切.
相切.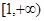 内的一切实数
内的一切实数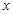 ,不等式
,不等式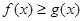 恒成立,求实数
恒成立,求实数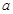 的取值范围;
的取值范围;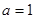 时,求最大的正整数
时,求最大的正整数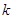 ,使得任意
,使得任意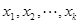
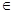
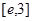 (
(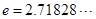 是自然对数的底数)都有
是自然对数的底数)都有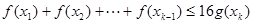 成立;
成立;
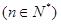 .
. ,其中
,其中 ,曲线
,曲线 在点
在点 处的切线垂直于
处的切线垂直于 轴.
轴. 的值;
的值; 的极值.
的极值.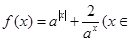 R,
R,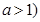 ,
,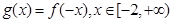 ,若
,若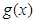 的最小值与
的最小值与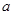 无关,求
无关,求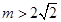 ,直接写出(不需给出演算步骤)关于
,直接写出(不需给出演算步骤)关于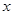 的方程
的方程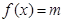 的解集
的解集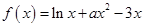 ,且在
,且在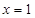 时函数取得极值.
时函数取得极值. 的单调增区间;
的单调增区间;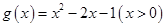 ,
,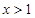 时,
时, 的图象恒在
的图象恒在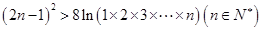 恒成立.
恒成立.