题目内容
如图，PA⊥矩形ABCD所在平面，M、N分别是AB、PC的中点.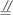
（1）求证MN∥平面PAD；
（2）求证MN⊥CD；
（3）若∠PDA=
，求证MN⊥平面PCD.
证明：（1）取PD中点E连NE、AE则NE
CD,AM
CD
∴AM
NE.AMNE为平行四边形，MN∥AE.
MN
面PAD，AE
面PAD.∴MN∥面PAD.
（2）CD⊥PA,CD⊥AD,∴CD⊥面PAD∴CD⊥AE，又MN∥AE,
∴CD⊥MN.
（3）∠PDA=
,∴PA=AD.则AE⊥PD,∴MN⊥PD.
又MN⊥CD,∴MN⊥面PCD.
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
如图，PA⊥矩形ABCD所在平面，PA=AD=a，M，N分别是AB，PC的中点，
如图，PA⊥矩形ABCD所在的平面，M，N分别是AB，PC的中点．
如图，PA⊥矩形ABCD所在的平面，M，N分别是PC，PA的中点，且PA=AB=2AD．
（2010•衢州一模）如图，PA⊥矩形ABCD所在的平面，M、N分别是AB、PC的中点．