题目内容
已知曲线
（θ为参数），曲线
（t为参数），则C1与C2
- A.没有公共点
- B.有一个公共点
- C.有两个公共点
- D.有两个以上的公共点
C
分析：先把两曲线的参数方程消去参数化为普通方程，再将圆心到直线的距离与半径作比较，判断
直线和圆的位置关系．
解答：把曲线（θ为参数）消去参数化为普通方程为 （x-1）2+y2=1，
表示一个以（1，0）为圆心，以1为半径的圆．
曲线（t为参数），即x+y-2=0，表示一条直线．
圆心到直线的距离等于
=
＜半径1，故两曲线有两个公共点．
故选 C．
点评：本题考查把参数方程化为普通方程的方法，点到直线的距离公式的应用．
分析：先把两曲线的参数方程消去参数化为普通方程，再将圆心到直线的距离与半径作比较，判断
直线和圆的位置关系．
解答：把曲线
（θ为参数）消去参数化为普通方程为 （x-1）2+y2=1，表示一个以（1，0）为圆心，以1为半径的圆．
曲线
（t为参数），即x+y-2=0，表示一条直线．圆心到直线的距离等于
=＜半径1，故两曲线有两个公共点．故选 C．
点评：本题考查把参数方程化为普通方程的方法，点到直线的距离公式的应用．
练习册系列答案
名校课堂系列答案
相关题目
：
(t为参数)与曲线
：
(
为参数，
) 有一个公共点在X轴上，则
.
：
（
为参数），
：
（
为参数）.
对应的参数为
，
为曲线
中点
到直线
：
（
小值.
（t为参数），
，C
的方程为普通方程，并说明它们分别表示什么曲线；
，Q为C
中点
到直线
（t为参数）距离的最小值。
：
(t为参数)与曲线
：
(
为参数，
) 有一个公共点在X轴上，则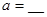
.
：
（
为参数），
：
（
为参数）.
对应的参数为
，
为曲线
中点
到直线
：
（