题目内容
等差数列{an}中,前n项和为Sn,若a7=5,S7=21,那么S10等于________.
40
分析:根据a7=5,S7=21,利用等差数列的通项公式得到关于首项和公差的两个方程,联立求出首项和公差,根据求出的首项与公差,利用等差数列的前n项和的公式求出S10即可.
解答:根据a7=5,S7=21得:a1+6d=5,7a1+ =21,解得 a1=1,d=
=21,解得 a1=1,d= .
.
∴S10=10a1+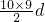 =40,
=40,
故答案为 40.
点评:本题考查等差数列的通项公式,等差数列的前n项和公式的应用,此题要求学生灵活运用等差数列的通项公式及前n项和的公式化简求值,是一道中档题.
分析:根据a7=5,S7=21,利用等差数列的通项公式得到关于首项和公差的两个方程,联立求出首项和公差,根据求出的首项与公差,利用等差数列的前n项和的公式求出S10即可.
解答:根据a7=5,S7=21得:a1+6d=5,7a1+
 =21,解得 a1=1,d=
=21,解得 a1=1,d= .
.∴S10=10a1+
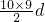 =40,
=40,故答案为 40.
点评:本题考查等差数列的通项公式,等差数列的前n项和公式的应用,此题要求学生灵活运用等差数列的通项公式及前n项和的公式化简求值,是一道中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目