题目内容
(本题满分13分)已知数列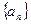 满足
满足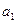 =-1,
=-1,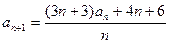 ,数列
,数列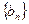 满足
满足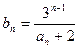
(1)求证:数列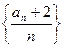 为等比数列,并求数列
为等比数列,并求数列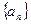 的通项公式.
的通项公式.
(2)求证:当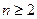 时,
时,
(3)设数列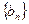 的前
的前 项和为
项和为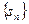 ,求证:当
,求证:当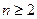 时,
时,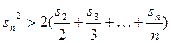 .
.
解:(1)由题意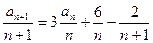 ,即
,即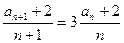
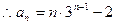 ………………………………4分
………………………………4分
(2)当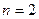 时,
时,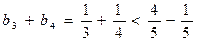 即
即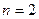 时命题成立
时命题成立
假设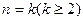 时命题成立,
时命题成立,
即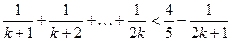
当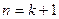 时,
时,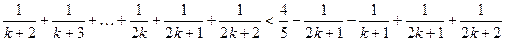
=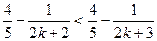 即
即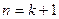 时命题也成立
时命题也成立
综上,对于任意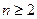 ,
, ………………8分
………………8分
(2)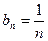 当
当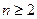 时,
时,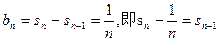
平方则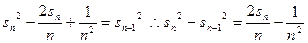
叠加得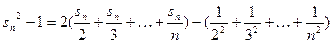
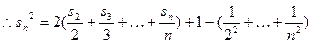
 ……………………………………13
……………………………………13 分
分
解析

练习册系列答案
相关题目
 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.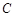 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 时,过点
时,过点 的直线
的直线 交曲线
交曲线 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.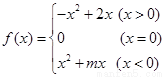 为奇函数;
为奇函数;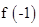 以及m的值;
以及m的值; 的图象;
的图象;
 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线
 取得最小值时点P的坐标.
取得最小值时点P的坐标.  是
是 轴上的动点,
轴上的动点, 分别切圆
分别切圆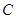 于
于 两点
两点 ,求直线
,求直线 的方程;
的方程; 恒过一定点.
恒过一定点.