题目内容
函数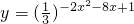 (-3≤x≤1)的值域是________,单调递增区间是________.
(-3≤x≤1)的值域是________,单调递增区间是________.
[3-9,39] (-2,+∞)
分析:可以看做是由y= 和t=-2x2-8x+1,两个函数符合而成,第一个函数是一个单调递减函数,要求原函数的值域,只要求出t=-2x2-8x+1,在[1,3]上的值域就可以,再根据同增异减点的单调区间.
和t=-2x2-8x+1,两个函数符合而成,第一个函数是一个单调递减函数,要求原函数的值域,只要求出t=-2x2-8x+1,在[1,3]上的值域就可以,再根据同增异减点的单调区间.
解答: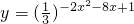
可以看做是由y= 和t=-2x2-8x+1,两个函数符合而成,
和t=-2x2-8x+1,两个函数符合而成,
第一个函数是一个单调递减函数,
要求原函数的值域,只要求出t=-2x2-8x+1,在[1,3]上的值域就可以,
t∈[-9,9]
此时y∈[3-9,39]
函数的递增区间是(-∞,-2],
故答案为:[3-9,39];(-2,+∞)
点评:本题考查指数型复合函数,求此类的函数的值域要分两步求解,第一步求出内层函数在定义域上的值域,第二步求外层函数在内层函数值域上的值域,这是解本题的关键,本题即是采取的这种技巧,求复合函数的值域一般采用本题的解法,思维量小,降低了单调性判断的难度,做此类题时要注意这一技巧的使用.
分析:可以看做是由y=
 和t=-2x2-8x+1,两个函数符合而成,第一个函数是一个单调递减函数,要求原函数的值域,只要求出t=-2x2-8x+1,在[1,3]上的值域就可以,再根据同增异减点的单调区间.
和t=-2x2-8x+1,两个函数符合而成,第一个函数是一个单调递减函数,要求原函数的值域,只要求出t=-2x2-8x+1,在[1,3]上的值域就可以,再根据同增异减点的单调区间.解答:
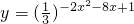
可以看做是由y=
 和t=-2x2-8x+1,两个函数符合而成,
和t=-2x2-8x+1,两个函数符合而成,第一个函数是一个单调递减函数,
要求原函数的值域,只要求出t=-2x2-8x+1,在[1,3]上的值域就可以,
t∈[-9,9]
此时y∈[3-9,39]
函数的递增区间是(-∞,-2],
故答案为:[3-9,39];(-2,+∞)
点评:本题考查指数型复合函数,求此类的函数的值域要分两步求解,第一步求出内层函数在定义域上的值域,第二步求外层函数在内层函数值域上的值域,这是解本题的关键,本题即是采取的这种技巧,求复合函数的值域一般采用本题的解法,思维量小,降低了单调性判断的难度,做此类题时要注意这一技巧的使用.

练习册系列答案
相关题目