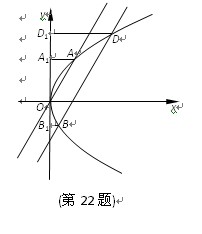
题目内容
(本题满分15分)过点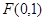 作直线
作直线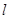 与抛物线
与抛物线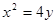 相交于两点
相交于两点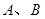 ,圆
,圆
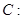
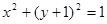
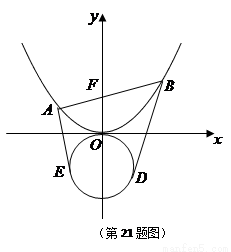
(Ⅰ)若抛物线在点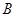 处的切线恰好与圆
处的切线恰好与圆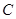 相切,求直线
相切,求直线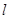 的方程;
的方程;
(Ⅱ)过点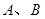 分别作圆
分别作圆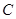 的切线
的切线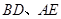 ,试求
,试求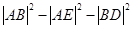 的取值范围.
的取值范围.
(I)直线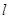 的方程为:
的方程为: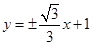 .(Ⅱ)
.(Ⅱ)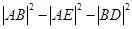 的取值范围是
的取值范围是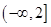 .
.
【解析】本试题主要是考查了直线与抛物线于圆与直线的位置关系的综合运用。以及导数的几何意义的运用,以及勾股定理的综合运用。
(1)利用导数的几何意义表示切线方程,以及直线与圆相切,则圆心到直线的距离为圆的半径可以得到结论。
(2)设出直线与抛物线联立方程组,结合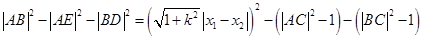
和韦达定理得到坐标关系,然后求解取值范围。
解:设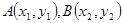
由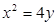 ,得
,得 过点
过点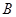 的切线方程为:
的切线方程为:
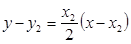 ,即
,即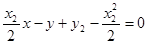 (3分)
(3分)
由已知: ,又
,又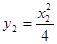 ,
(5分)
,
(5分)
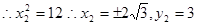 ,
,
即点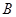 坐标为
坐标为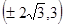 ,
(6分)
,
(6分)
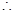 直线
直线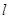 的方程为:
的方程为: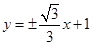 . (7分)
. (7分)
(Ⅱ)由已知,直线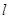 的斜率存在,则设直线
的斜率存在,则设直线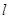 的方程为:
的方程为: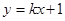 , (8分)
, (8分)
联立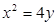 ,得
,得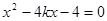
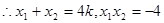
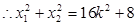 (9分)
(9分)
解法一: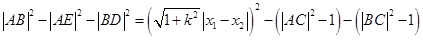 (12分)
(12分)


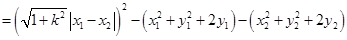
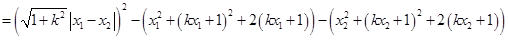 (13分)
(13分)
 =
=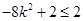 (15分)
(15分)
解法二: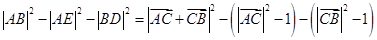 (12分)
(12分)
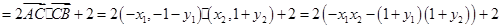
 (13分)
(13分)

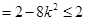 (15分)
(15分)
解法三: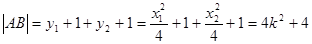 ,
,
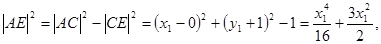
同理,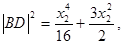 (13分)
(13分)
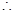
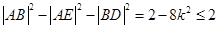
故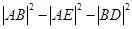 的取值范围是
的取值范围是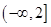 .
(15分)
.
(15分)

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
 中,
中, 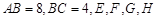 分别为四边
分别为四边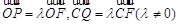 .
.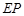 与
与 的交点
的交点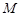 的轨迹
的轨迹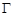 的方程;
的方程;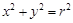
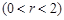 上一点
上一点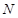 作圆的切线与轨迹
作圆的切线与轨迹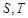 两点,若
两点,若 ,试求出
,试求出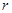 的值.
的值.

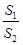 的取值范围.
的取值范围.