题目内容
【题目】已知函数![]() ,
, ![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,使得
,使得![]() 的解集恰好是
的解集恰好是![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() ;(2)符合要求的整数
;(2)符合要求的整数![]() 是
是 或
或 .
.
【解析】试题分析:(1)求出函数的对称轴,由于y=|f(x)|在[﹣1,0]上是减函数,则讨论区间在对称轴的右边,且f(0)不小于0,区间在对称轴的左边,且f(0)不大于0.解出它们即可;
(2)假设存在整数a,b,使得a≤f(x)≤b的解集恰好是[a,b].则f(a)=a,f(b)=a,a≤f(![]() )≤b,由f(a)=f(b)=a,解出整数a,b,再代入不等式检验即可.
)≤b,由f(a)=f(b)=a,解出整数a,b,再代入不等式检验即可.
试题解析:
(1)令![]() ,则
,则![]() .
.
当![]() ,即
,即![]() 时,
时, ![]() 恒成立,
恒成立,
所以![]() .
.
因为![]() 在
在![]() 上是减函数,
上是减函数,
所以![]() ,解得
,解得![]() ,
,
所以![]() .
.
由![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时, ![]() 的图象对称轴
的图象对称轴![]() ,
,
且方程![]() 的两根均为正,
的两根均为正,
此时![]() 在
在![]() 为减函数,所以
为减函数,所以![]() 符合条件.
符合条件.
当![]() 时,
时, ![]() 的图象对称轴
的图象对称轴![]() ,
,
且方程![]() 的根为一正一负,
的根为一正一负,
要使![]() 在
在![]() 单调递减,则
单调递减,则![]() ,解得
,解得![]() .
.
综上可知,实数![]() 的取值范围为
的取值范围为![]() .
.
(2)假设存在整数![]() ,使
,使![]() 的解集恰好是
的解集恰好是![]() ,则
,则
①若函数![]() 在
在![]() 上单调递增,则
上单调递增,则![]() ,
, ![]() 且
且![]() ,
,
即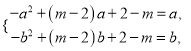
作差得到![]() ,代回得到:
,代回得到: ![]() ,即
,即![]() ,由于
,由于![]() 均为整数,
均为整数,
故![]() ,
, ![]() ,
, ![]() 或
或![]() ,
, ![]() ,
, ![]() ,经检验均不满足要求;
,经检验均不满足要求;
②若函数![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,
, ![]() 且
且![]() ,
,
即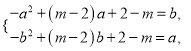
作差得到![]() ,代回得到:
,代回得到: ![]() ,即
,即![]() ,由于
,由于![]() 均为整数,
均为整数,
故![]() ,
, ![]() ,
, ![]() 或
或![]() ,
, ![]() ,
, ![]() ,经检验均不满足要求;
,经检验均不满足要求;
③若函数![]() 在
在![]() 上不单调,则
上不单调,则![]() ,
, ![]() 且
且![]() ,
,
即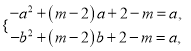 作差得到
作差得到![]() ,代回得到:
,代回得到: ![]() ,即
,即![]() ,由于
,由于![]() 均为整数,
均为整数,
故![]() ,
, ![]() ,
, ![]() 或
或![]() ,
, ![]() ,
, ![]() ,,经检验均满足要求;
,,经检验均满足要求;
综上,符合要求的整数![]() 是
是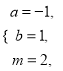 或
或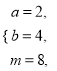

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目

