题目内容
f'（x0）=2，求| lim |
| △x→0 |
| f(x0-△x)-f(x0) |
| 2△x |
分析：先将
化成(-
)
，而f'（x0）=
，从而求出所求．
| lim |
| △x→0 |
| f(x0-△x)-f(x0) |
| 2△x |
| 1 |
| 2 |
| lim |
| △x→0 |
| f(x0-△x)-f(x0) |
| -△x |
| lim |
| △x→0 |
| f(x0-△x)-f(x0) |
| -△x |
解答：解：
=(-
)
=-
f'（x0）=-1
故答案为：-1
| lim |
| △x→0 |
| f(x0-△x)-f(x0) |
| 2△x |
| 1 |
| 2 |
| lim |
| △x→0 |
| f(x0-△x)-f(x0) |
| -△x |
| 1 |
| 2 |
故答案为：-1
点评：本题主要考查了导数的定义，同时考查了导数的意义，属于基础题．
练习册系列答案
相关题目
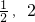]上的值域．