题目内容
已知
，
是二次函数，
是奇函数，且当x∈[-1，2]时，
的最小值是1，求
的表达式。
，
是二次函数，
是奇函数，且当x∈[-1，2]时，
的最小值是1，求
的表达式。 解：设
，
则
，
又
为奇函数，
∴
对x∈R恒成立，
∴
，解得
，
∴
，其对称轴为
，
（1）当
即b>2时，
，
∴b=3；
（2）当
即
时，
，
解得：
或
（舍去）；
（3）当
即b<-4时，
，
∴b=-3（舍去），
综上可知，
或
。
，则
，又
为奇函数，∴
对x∈R恒成立，∴
，解得
，∴
，其对称轴为
，（1）当
即b>2时，
，∴b=3；
（2）当
即
时，
，解得：
或
（舍去）；（3）当
即b<-4时，
，∴b=-3（舍去），
综上可知，
或
。
练习册系列答案
阅读快车系列答案
相关题目
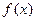是二次函数，且f(0)=8及f(x+1)－f(x)＝－2x+1
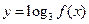的单调递减区间及值域..
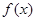是二次函数，不等式
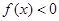的解集是
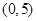，且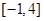
上的最大值为12．
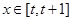上的最小值为
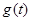，求
，
是二次函数，
是奇函数，且当
时，