题目内容
已知定义在 上的函数
上的函数 是奇函数且满足
是奇函数且满足 ,
, ,数列
,数列 满足
满足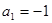 ,且
,且 ,(其中
,(其中 为
为 的前
的前 项和),则
项和),则 ( ).
( ).
A. | B. | C. | D. |

解析试题分析:∵函数 是奇函数
是奇函数 ,
,
∴ 是以3为周期的周期函数.
是以3为周期的周期函数.
两式相减并整理得出 ,即
,即 ,
,
∴数列 是以2为公比的等比数列,首项为
是以2为公比的等比数列,首项为 ,
,
 ,故选
,故选 .
.
考点:函数的奇偶性与周期性,等比数列的通项公式.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
函数 的零点所在的区间是( )
的零点所在的区间是( )
A. | B. | C.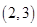 | D. |
为了得到函数 的图象,只需把函数
的图象,只需把函数 图象上的所有点( )
图象上的所有点( )
| A.纵坐标伸长到原来的2倍,横坐标不变 | B.横坐标伸长到原来的2倍,纵坐标不变 |
C.纵坐标缩短到原来的 倍,横坐标不变 倍,横坐标不变 | D.横坐标缩短到原来的 倍,纵坐标不变 倍,纵坐标不变 |
设函数 的定义域为
的定义域为 ,如果存在正实数
,如果存在正实数 ,对于任意
,对于任意 ,都有
,都有 ,且
,且 恒成立,则称函数
恒成立,则称函数 为
为 上的“
上的“ 型增函数”,已知函数
型增函数”,已知函数 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当 时,
时, ,若
,若 为
为 上的“2014型增函数”,则实数
上的“2014型增函数”,则实数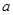 的取值范围是( )
的取值范围是( )
A. | B. | C.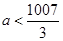 | D.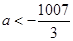 |
已知函数 ,若存在实数
,若存在实数 满足
满足 ,且
,且 ,则
,则 的取值范围( )
的取值范围( )
| A.(20,32) | B.(9,21) | C.(8,24) | D.(15,25) |
下列函数中,既是偶函数,又在区间 内是增函数的为( )
内是增函数的为( )
A. | B. |
C. | D. |
定义在R上的奇函数 满足
满足 ,且在
,且在 上是增函数,则有( )
上是增函数,则有( )
A.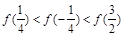 | B. |
C. | D. |
设 为定义在R上的奇函数,当
为定义在R上的奇函数,当 时,
时, (b为常数),则
(b为常数),则 ( )
( )
| A.3 |
| B.1 |
C. |
D. |
函数 是奇函数的充要条件是
是奇函数的充要条件是
A. | B. | C. | D. |